
【题目】已知![]() ,
, ![]() ,
, ![]() ,斜率为
,斜率为![]() 的直线
的直线![]() 过点
过点![]() ,且
,且![]() 和以
和以![]() 为圆
为圆![]() 相切.
相切.
(1)求圆![]() 的方程;
的方程;
(2)在圆![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ,若存在,求出所有的点
,若存在,求出所有的点![]() 的坐标;若不存在说明理由;
的坐标;若不存在说明理由;
(3)若不过![]() 的直线
的直线![]() 与圆
与圆![]() 交于
交于![]() ,
, ![]() 两点,且满足
两点,且满足![]() ,
, ![]() ,
, ![]() 的斜率依次为等比数列,求直线
的斜率依次为等比数列,求直线![]() 的斜率.
的斜率.
【答案】(1)![]() (2)
(2)![]() 或
或![]() ;(3)
;(3)![]()
【解析】试题分析:根据直线与圆C相切,则点C到直线![]() 的距离为圆的半径,写出圆的方程;设点P的坐标,根据已知条件表示
的距离为圆的半径,写出圆的方程;设点P的坐标,根据已知条件表示![]() ,与圆的方程联立方程组,解方程组求出点P的坐标;存在性问题是高考高频考点,首先假设直线存在,分直线m的斜率不存在和存在两种情况研究,若存在不妨设为k,根据要求求出斜率k的值,得出这样的直线存在,给出斜率k.
,与圆的方程联立方程组,解方程组求出点P的坐标;存在性问题是高考高频考点,首先假设直线存在,分直线m的斜率不存在和存在两种情况研究,若存在不妨设为k,根据要求求出斜率k的值,得出这样的直线存在,给出斜率k.
试题解析:
(1)![]() :
: ![]() ,
,
∵直线![]() 和圆
和圆![]() 相切∴设圆
相切∴设圆![]() 的半径为
的半径为![]() ,则
,则![]() ,
,
∴圆![]() :
: ![]() ;
;
(2)设![]() ,则由
,则由![]() ,得
,得![]() ,
,
又∵点![]() 在圆
在圆![]() 上,∴
上,∴![]() ,
,
相减得: ![]() ,
,
代入![]() ,得
,得![]() ,
,
解得![]() 或
或![]() ,
,
∴点的坐标为![]() 或
或![]() ;
;
(3)若直![]() 线
线![]() 的斜率不存在,则
的斜率不存在,则![]() 的斜率也不存在,不合题意:
的斜率也不存在,不合题意:
设直线![]() :
: ![]() ,
, ![]() ,
, ![]() ,
,
直线![]() 与圆
与圆![]() 联立,得
联立,得![]() ,
,
由![]() ,得
,得![]() ,
,
即![]() 。
。
整理得: ![]() ,
,
∵![]() 不过
不过![]() 点,∴
点,∴![]() ,∴上式化为
,∴上式化为![]() .
.
将![]() 代入得:
代入得: ![]() ,
,
即![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∴直线![]() 的斜率为
的斜率为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)满足f(x)=x2﹣2(a+2)x+a2 , g(x)=﹣x2+2(a﹣2)x﹣a2+8.设H1(x)=max{f(x),g(x)},H2(x)=min{f(x),g(x)}(max(p,q)表示p,q中的较大值,min(p,q)表示p,q中的较小值),记H1(x)的最小值为A,H2(x)的最大值为B,则A﹣B=( )
A.a2﹣2a﹣16
B.a2+2a﹣16
C.-16
D.16
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣2ax+2,x∈[﹣5,5]
(1)求实数a的取值范围,使y=f(x)在定义域上是单调递减函数;
(2)用g(a)表示函数y=f(x)的最小值,求g(a)的解析式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校在一次第二课堂活动中,特意设置了过关智力游戏,游戏共五关.规定第一关没过者没奖励,过![]()
![]() 关者奖励
关者奖励![]() 件小奖品(奖品都一样).下图是小明在10次过关游戏中过关数的条形图,以此频率估计概率.
件小奖品(奖品都一样).下图是小明在10次过关游戏中过关数的条形图,以此频率估计概率.
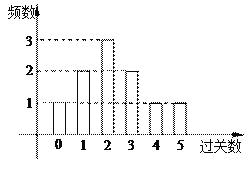
(Ⅰ)估计小明在1次游戏中所得奖品数的期望值;
(Ⅱ)估计小明在3 次游戏中至少过两关的平均次数;
(Ⅲ)估计小明在3 次游戏中所得奖品超过30件的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的方程是
的方程是![]() ,双曲线
,双曲线![]() 的左右焦点分别为
的左右焦点分别为![]() 的左右顶点,而
的左右顶点,而![]() 的左右顶点分别是
的左右顶点分别是![]() 的左右焦点.
的左右焦点.
(1)求双曲线![]() 的方程;
的方程;
(2)若直线![]() 与双曲线
与双曲线![]() 恒有两个不同的交点,且
恒有两个不同的交点,且![]() 与
与![]() 的两个交点A和B满足
的两个交点A和B满足![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com