
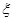 ,求概率P
,求概率P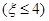 .
.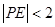 的概率.
的概率.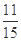 ;(2)
;(2) 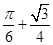
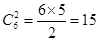 种情况,而其中两个点之间的距离的平方大于4的情况有4种,所以符合题意的共有11种,即可得到结论.本小题考查古典概型的问题,“正难则反”,也是这类题中的一种解题方法.
种情况,而其中两个点之间的距离的平方大于4的情况有4种,所以符合题意的共有11种,即可得到结论.本小题考查古典概型的问题,“正难则反”,也是这类题中的一种解题方法.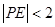 的概率,即需要求出点P所围成的面积,通过求出一个扇形与两个直角三角形的面积和,即可求得结论.
的概率,即需要求出点P所围成的面积,通过求出一个扇形与两个直角三角形的面积和,即可求得结论.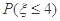 =
=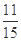
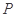 构成的平面区域是正方形
构成的平面区域是正方形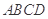 的内部,其面积是
的内部,其面积是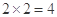 .满足
.满足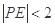 的点
的点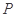 构成的平面区域是以
构成的平面区域是以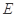 为圆心,2为半径的圆的内部与正方形
为圆心,2为半径的圆的内部与正方形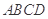 内部的公共部分,它可以看作是由一个以
内部的公共部分,它可以看作是由一个以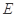 为圆心、2为半径、圆心角为
为圆心、2为半径、圆心角为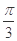 的扇形的内部与两个直角边分别为1和
的扇形的内部与两个直角边分别为1和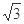 的直角三角形内部构成.其面积是
的直角三角形内部构成.其面积是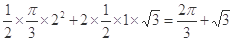 .
.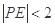 的概率为
的概率为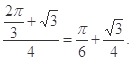


科目:高中数学 来源:不详 题型:解答题
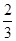 ,乙队获胜的概率为
,乙队获胜的概率为 ,假设每场比赛的结果互相独立.现已赛完两场,乙队以
,假设每场比赛的结果互相独立.现已赛完两场,乙队以 暂时领先.
暂时领先. ,求随机变量
,求随机变量 的分布列和数学期望
的分布列和数学期望 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.n=3 | B.n=4 | C.n=9 | D.n=10 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
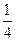 ,乙机床加工的零件是一等品而丙机床加工的零件不是一等品的概率为
,乙机床加工的零件是一等品而丙机床加工的零件不是一等品的概率为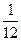 ,甲、丙两台机床加工的零件都是一等品的概率为
,甲、丙两台机床加工的零件都是一等品的概率为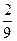 .则丙机床加工的零件是一等品的概率为( )
.则丙机床加工的零件是一等品的概率为( )A.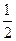 | B.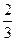 | C.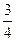 | D.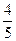 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题

| A.0.35 | B.0.45 | C.0.55 | D.0.65 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com