Question

若f（x）=log_a（2-ax）在[0，1]上是减函数，则a的取值范围是________．

Answer 1

1＜a＜2
分析：本题必须保证：①使log_a（2-ax）有意义，即a＞0且a≠1，2-ax＞0．②使log_a（2-ax）在[0，1]上是x的减函数．由于所给函数可分解为y=log_au，u=2-ax，其中u=2-ax在a＞0时为减函数，所以必须a＞1；③[0，1]必须是y=log_a（2-ax）定义域的子集．
解答：因为f（x）在[0，1]上是x的减函数，所以f（0）＞f（1），
即log_a2＞log_a（2-a）．
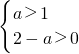
∴?1＜a＜2
故答案为：1＜a＜2．
点评：本题综合了多个知识点，需要概念清楚，推理正确．（1）复合函数的单调性；（2）真数大于零．