
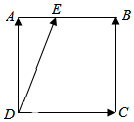
 如图,己知正方形ABCD的边长为l,点E是AB边上的动点.
如图,己知正方形ABCD的边长为l,点E是AB边上的动点.分析 以D为坐标原点建立平面直角坐标系,得到D,A,B,C,以及对应向量的坐标,进行数量积的运算求值即可.
解答 解:以D为坐标原点建立平面直角坐标系,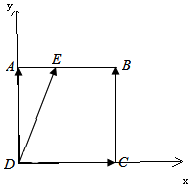 则D(0,0),A(0,1)B(1,1),C(1,0),设E(x,y),则$\overrightarrow{DE}$=(x,1),$\overrightarrow{CB}$=(0,1),
则D(0,0),A(0,1)B(1,1),C(1,0),设E(x,y),则$\overrightarrow{DE}$=(x,1),$\overrightarrow{CB}$=(0,1),
所以(1)$\overrightarrow{DE}$•$\overrightarrow{CB}$=1 (6分)
(2)$\overrightarrow{DC}$=(1,0),所以$\overrightarrow{DE}$•$\overrightarrow{DC}$=x,又0≤x≤1,所以$\overrightarrow{DE}$•$\overrightarrow{DC}$ 的最大值为1.(12分)
点评 本题考查了平面向量的数量积运算;借助于坐标运算使得计算简便.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com