Question

已知函数f(x)＝x³－3ax²－9a²x＋a³.

(1)设a＝1，求函数f(x)的极值；

(2)若a>，且当x∈[1,4a]时，|f′(x)|≤12a恒成立，试确定a的取值范围．

 

Answer 1

【答案】

（1）f(x)的极大值是f(－1)＝6，极小值是f(3)＝－26.；（2）(，]．

【解析】(1)利用导数利用确定极值即可。

(2)解本题的关键是|f′(x)|≤12a转化为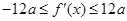恒成立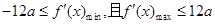，.然后解不等式组求解即可。

解：(1)当a＝1时，对函数f(x)求导数，得f′(x)＝3x²－6x－9.令f′(x)＝0，解得

x₁＝－1，x₂＝3.

列表讨论f(x)，f′(x)的变化情况：

x	(－∞，－1)	－1	(－1,3)	3	(3，＋∞)
f′(x)	＋	0	－	0	＋
f(x)	?	极大 值6	?	极小 值－26	?

所以，f(x)的极大值是f(－1)＝6，极小值是f(3)＝－26.                  5分

(2)f′(x)＝3x²－6ax－9a²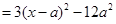的图象是一条开口向上的抛物线，

关于x＝a对称．   若<a≤1，则f′(x)在[1,4a]上是增函数，从而f′(x)在[1,4a]上的最小值是f′(1)＝3－6a－9a²，            最大值是f′(4a)＝15a².

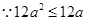
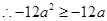          ∴必有f′(1)＝3－6a－9a²≥－12a，∴只要有f′(4a)＝15a²≤12a.    得0≤a≤.

所以a∈(，1]∩[0，]，    即a∈(，]．                           11分

 若a>1，则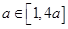 ∵|f′(a)|＝12a²>12a.

故当x∈[1,4a]时|f′(x)|≤12a不恒成立．

所以使|f′(x)|≤12a(x∈[1,4a])恒成立的a的取值范围是(，]．         14分