
已知函数f(x)= -ln(x+m).
-ln(x+m).
(Ι)设x=0是f(x)的极值点,求m,并讨论f(x)的单调性;
(Ⅱ)当m≤2时,证明f(x)>0.
(Ι) 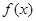 在
在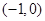 上是减函数;在
上是减函数;在 上是增函数(Ⅱ)见解析
上是增函数(Ⅱ)见解析
【解析】(Ι)因为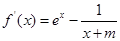 ,
x=0是f(x)的极值点,所以
,
x=0是f(x)的极值点,所以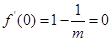 ,解得
,解得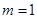 ,
,
所以函数f(x)=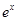 -ln(x+1),其定义域为
-ln(x+1),其定义域为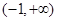 ,因为
,因为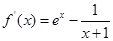 =
=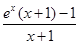 ,
,
设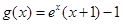 ,则
,则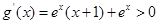 ,所以
,所以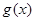 在
在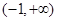 上是增函数,又因为
上是增函数,又因为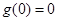 ,所以当
,所以当 时,
时,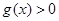 ,即
,即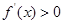 ;当
;当 时,
时,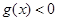 ,
,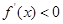 ,所以
,所以
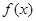 在
在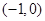 上是减函数;在
上是减函数;在 上是增函数.
上是增函数.
(Ⅱ)当m≤2,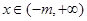 时,
时, ,故只需证明当
,故只需证明当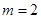 时,
时,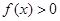 .
.
当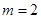 时,函数
时,函数 在
在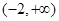 单调递增,
单调递增,
又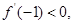
 故
故 在
在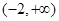 有唯一实根
有唯一实根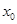 ,且
,且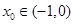 ,
,
当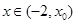 时,
时,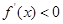 ;当
;当 时,
时,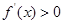 ,从而当
,从而当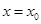 时,
时,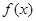 取得最小值,
取得最小值,
由 得:
得: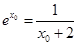 ,即
,即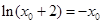 ,
,
故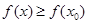 =
=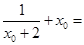
 ,
,
综上,当m≤2时,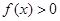 .
.
本题第(Ⅰ)问,由极值点得出,在x=0处的导数等于0,求出m值;对单调性,而判断导数的正负号,从而需构造函数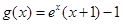 ,通过判断函数
,通过判断函数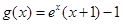 的单调性,来得出
的单调性,来得出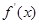 的正负,从而求得结果; 对第(Ⅱ)问,要证明
的正负,从而求得结果; 对第(Ⅱ)问,要证明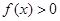 ,只需要证明
,只需要证明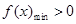 即可.对第(Ι)问,函数单调性的讨论,一部分想不到构造函数
即可.对第(Ι)问,函数单调性的讨论,一部分想不到构造函数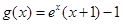 ;对第(Ⅱ)问,证明不等式,找不到思路.
;对第(Ⅱ)问,证明不等式,找不到思路.
【考点定位】本小题主要考查利用导数研究函数的单调性、极值、最值、证明不等式等知识,综合性较强,考查函数与方程、分类讨论等数学思想,考查同学们分析问题、解决问题的能力,熟练函数与导数的基础知识以及基本题型是解答好本类题目的关键.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:高中数学 来源: 题型:
|
| 1 |
| π |
查看答案和解析>>
科目:高中数学 来源: 题型:
 已知函数f(x)=
已知函数f(x)=
|
A、(
| ||||
B、(
| ||||
C、(
| ||||
D、[
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| x-1 | x+a |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com