
【题目】如图,多面体![]() 中,
中, ![]() 两两垂直,平面
两两垂直,平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
, ![]() .
.
(1)证明四边形![]() 是正方形;
是正方形;
(2)判断点![]() 是否四点共面,并说明为什么?
是否四点共面,并说明为什么?
(3)连结![]() ,求证:
,求证: ![]() 平面
平面![]() .
.
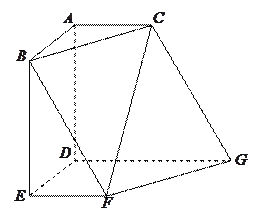
【答案】(1)见解析;(2)共面,见解析;(3)见解析
【解析】试题分析:(1)要证明四边形是一个正方形,首先证明四边形是一个平行四边形,这里应用两个平面平行的性质定理,再根据一对邻边相等,得到正方形.
(2)要判断四点共面,只要判断三点共面,再证明第四个点在平面上,或者是证明四点在两条平行的直线上,选择后者,进行证明.
(3)要证明限于面垂直只要证明这条线与平面上的两条相交直线垂直,解题的关键是找出这两条线,选择了BG和BD这两条相交直线,得到结论.
试题解析:
证明:(1) ,
,
同理AD∥BE,
则四边形ABED是平行四边形.
又AD⊥DE,AD=DE,
∴四边形ABED是正方形
(2)取DG中点P,连接PA,PF.
在梯形EFGD中,FP∥DE且FP=DE.
又AB∥DE且AB=DE,∴AB∥PF且AB=PF
∴四边形ABFP为平行四边形,
∴AP∥BF
在梯形ACGD中,AP∥CG,∴BF∥CG,
∴B,C,F,G四点共面
(3)同(1)中证明方法知四边形BFGC为平行四边形.
且有AC∥DG、EF∥DG,从而AC∥EF,
∴EF⊥AD,BE∥AD
又BE=AD=2、EF=1故![]() ,而
,而![]() ,
,
故四边形BFGC为菱形,CF⊥BG
又由AC∥EF且AC=EF知CF∥AE.
正方形ABED中,AE⊥BD,故CF⊥BD.
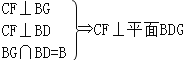


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知点P(x、y)满足
(1)若x∈{0,1,2,3,4,5},y∈{0,1,2,3,4},则求y≥x的概率.
(2)若x∈[0,5],y∈[0,4],则求x>y的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在多面体![]() 中,底面
中,底面![]() 是边长为
是边长为![]() 的菱形,
的菱形, ![]() ,四边形
,四边形![]() 是矩形,平面
是矩形,平面![]() 平面
平面![]() ,
, ![]() ,
, ![]() 是
是![]() 的中点.
的中点.

(1)求证: ![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(3)求二面角![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知{an}为等差数列,a1+a3+a5=105,a2+a4+a6=99,以Sn表示{an}的前n项和,则使得Sn达到最大值的n是( )
A.21
B.20
C.19
D.18
查看答案和解析>>
科目:高中数学 来源: 题型:
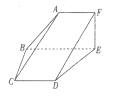
【题目】如图,平面![]() 平面
平面![]() 四边形
四边形![]() 为直角梯形,
为直角梯形, ![]() 四边形
四边形![]() 为等腰梯形,
为等腰梯形, ![]() 且
且![]()
(Ⅰ)若梯形![]() 内有一点
内有一点![]() ,使得
,使得![]() 平面
平面![]() ,求点
,求点![]() 的轨迹;
的轨迹;
(Ⅱ)求平面![]() 与平面
与平面![]() 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
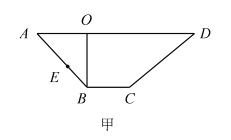
【题目】如图甲所示, ![]() 是梯形
是梯形![]() 的高,
的高, ![]() ,
, ![]() ,
, ![]() ,现将梯形
,现将梯形![]() 沿
沿![]() 折起如图乙所示的四棱锥
折起如图乙所示的四棱锥![]() ,使得
,使得![]() ,点
,点![]() 是线段
是线段![]() 上一动点.
上一动点.
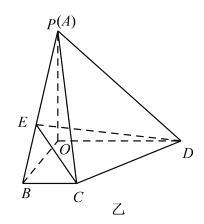
(1)证明: ![]() 和
和![]() 不可能垂直;
不可能垂直;
(2)当![]() 时,求
时,求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设直线![]() 与圆
与圆![]() 交于M、N两点,且M、N关于直线
交于M、N两点,且M、N关于直线![]() 对称.
对称.
(1)求m,k的值;
(2)若直线![]() 与圆C交P,Q两点,是否存在实数a使得OP⊥OQ,如果存在,求出a的值;如果不存在,请说明理由.
与圆C交P,Q两点,是否存在实数a使得OP⊥OQ,如果存在,求出a的值;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥![]() 中,底面为矩形,
中,底面为矩形, ![]() 底面
底面![]() ,
, ![]() ,
,
![]()
![]() 为
为![]() 中点.
中点.

(Ⅰ)在图中作出平面![]() 与
与![]() 的交点
的交点![]() ,并指出点
,并指出点![]() 所在位置(不要求给出理由);
所在位置(不要求给出理由);
(Ⅱ)在线段![]() 上是否存在一点
上是否存在一点![]() ,使得直线
,使得直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,若存在,请说明点
,若存在,请说明点![]() 的位置;若不存在,请说明理由;
的位置;若不存在,请说明理由;
(Ⅲ)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:x∈A,且A={x|a﹣1<x<a+1},命题q:x∈B,且B={x|x2﹣4x+3≥0}
(Ⅰ)若A∩B=,A∪B=R,求实数a的值;
(Ⅱ)若p是q的充分条件,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com