
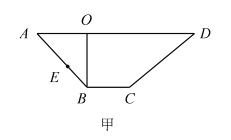
【题目】如图甲所示, ![]() 是梯形
是梯形![]() 的高,
的高, ![]() ,
, ![]() ,
, ![]() ,现将梯形
,现将梯形![]() 沿
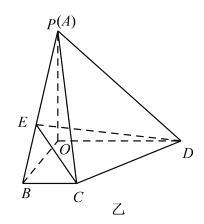
沿![]() 折起如图乙所示的四棱锥
折起如图乙所示的四棱锥![]() ,使得
,使得![]() ,点
,点![]() 是线段
是线段![]() 上一动点.
上一动点.
(1)证明: ![]() 和
和![]() 不可能垂直;
不可能垂直;
(2)当![]() 时,求
时,求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)详见解析; (2)![]() .
.
【解析】试题分析:由于折叠后![]() ,经过计算知
,经过计算知![]() ,这样
,这样![]() 两两垂直,因此以它们为坐标轴建立空间直角坐标系,写出各点坐标.
两两垂直,因此以它们为坐标轴建立空间直角坐标系,写出各点坐标.
(1)否定性命题,可假设![]() ,同时设
,同时设![]() (
(![]() ),利用向量垂直计算出
),利用向量垂直计算出![]() ,如果满足
,如果满足![]() 说明存在,如果不满足
说明存在,如果不满足![]() 说明不存在;
说明不存在;
(2)由![]() 得
得![]() 点坐标,从而可求出平面
点坐标,从而可求出平面![]() 的法向量
的法向量![]() ,则向量
,则向量![]() 与
与![]() 夹角的余弦的绝对值等于直线
夹角的余弦的绝对值等于直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
解析:如图甲所示,因为![]() 是梯形
是梯形![]() 的高,
的高,![]() ,所以
,所以![]() ,因为
,因为![]() ,
,![]() ,可得
,可得![]() ,
,![]() ,如图乙所示,
,如图乙所示,![]() ,
, ![]() ,
,![]() ,所以有
,所以有![]() ,所以
,所以![]() ,而
,而![]() ,
,![]() ,所以
,所以![]() 平面
平面![]() ,又
,又![]() ,所以
,所以![]() 、
、![]() 、
、![]() 两两垂直.故以
两两垂直.故以![]() 为原点,建立空间直角坐标系(如图),则
为原点,建立空间直角坐标系(如图),则![]() ,
,![]() ,
,![]() ,
,

(1)设![]() 其中
其中![]() ,所以
,所以![]() ,
,![]() ,假设
,假设![]() 和
和![]() 垂直,则
垂直,则![]() ,有
,有![]() ,解得
,解得![]() ,这与
,这与![]() 矛盾,假设不成立,所以
矛盾,假设不成立,所以![]() 和
和![]() 不可能垂直.
不可能垂直.
(2)因为![]() ,所以
,所以 ![]() ,设平面
,设平面![]() 的一个法向量是
的一个法向量是![]() ,因为
,因为![]() ,
,![]() ,所以
,所以![]() ,
,![]() ,即
,即 ,取
,取![]() ,而
,而![]() ,所以
,所以 ,所以
,所以![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(x﹣ ![]() )cos(x﹣
)cos(x﹣ ![]() )(x∈R),则下面结论错误的是( )
)(x∈R),则下面结论错误的是( )
A.函数f(x)的图象关于点(﹣ ![]() ,0)对称
,0)对称
B.函数f(x)的图象关于直线x=﹣ ![]() 对称
对称
C.函数f(x)在区间[0, ![]() ]上是增函数
]上是增函数
D.函数f(x)的图象是由函数y= ![]() sin2x的图象向右平移
sin2x的图象向右平移 ![]() 个单位而得到
个单位而得到
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种产品的广告费支出![]() (百万元)与销售额
(百万元)与销售额![]() (百万元)之间有如下对应数据:
(百万元)之间有如下对应数据:
| 2 | 4 | 5 | 6 | 8 |
| 30 | 40 | 50 | 60 | 70 |
如果![]() 与
与![]() 之间具有线性相关关系.
之间具有线性相关关系.
(1)作出这些数据的散点图;
(2)求这些数据的线性回归方程![]() ;
;
(3)预测当广告费支出为9百万元时的销售额。 ( 参考数据: ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设m,n是两条不同的直线,α、β是两个不同的平面,则下列命题不正确的是________.
(1).若m⊥n,m⊥α,n![]() α,则n∥α
α,则n∥α
(2).若m⊥β,α⊥β,则m∥α或m![]() α
α
(3).若m⊥n,m⊥α,n⊥β,则α⊥β
(4).若![]() ∥α,α⊥β,则
∥α,α⊥β,则![]() ⊥β
⊥β
查看答案和解析>>
科目:高中数学 来源: 题型:
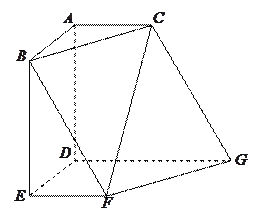
【题目】如图,多面体![]() 中,
中, ![]() 两两垂直,平面
两两垂直,平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
, ![]() .
.
(1)证明四边形![]() 是正方形;
是正方形;
(2)判断点![]() 是否四点共面,并说明为什么?
是否四点共面,并说明为什么?
(3)连结![]() ,求证:
,求证: ![]() 平面
平面![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】假设某种设备使用的年限x(年)与所支出的维修费用y(万元)有以下统计资料:
使用年限x | 2 | 3 | 4 | 5 | 6 |
维修费用y | 2 | 4 | 5 | 6 | 7 |
若由资料知y对x呈线性相关关系。试求:
(1)求![]() ; (2)线性回归方程
; (2)线性回归方程![]() ;
;
(3)估计使用10年时,维修费用是多少?
附:利用“最小二乘法”计算a,b的值时,可根据以下公式:

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设点M是棱长为2的正方体的棱AD的中点,P是平面![]() 内一点,若面
内一点,若面![]() 分别与面ABCD和面
分别与面ABCD和面![]() 所成的锐二面角相等,则
所成的锐二面角相等,则![]() 长度的最小值是( )
长度的最小值是( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 1
D. 1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com