
 的部分图象,直线
的部分图象,直线 是其两条对称轴.
是其两条对称轴.
 的解析式;
的解析式; 的单调增区间;
的单调增区间;  ,且
,且 ,求
,求 的值.
的值. ,(2)
,(2) ,(3)
,(3) .
. ,就是要确定
,就是要确定 由
由 知要确定
知要确定 就是要确定
就是要确定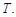 由三角函数图像知相邻两条对称轴之间距离为半个周期,所以
由三角函数图像知相邻两条对称轴之间距离为半个周期,所以 ,即
,即
 ;根据函数过点
;根据函数过点 且
且 ,求出
,求出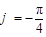 ,本题在求
,本题在求 时,注意点的选择,一般选最值点,不易取中间“零点”,因为经过“零点”的图像有两种趋势,这就使代入的点不能确定函数解析式;(2)求三角函数单调区间,实际上还是从图像上求解,即单调增区间就是从最小值点
时,注意点的选择,一般选最值点,不易取中间“零点”,因为经过“零点”的图像有两种趋势,这就使代入的点不能确定函数解析式;(2)求三角函数单调区间,实际上还是从图像上求解,即单调增区间就是从最小值点 ,增加到最大值
,增加到最大值 结合周期
结合周期 从而可得出单调增区间
从而可得出单调增区间 ,本题也可通过解不等式得到单调增区间,即
,本题也可通过解不等式得到单调增区间,即 (3)本题实际是给值求值三角函数问题,即已知
(3)本题实际是给值求值三角函数问题,即已知 ,求
,求 的值.解题关键是将欲求角
的值.解题关键是将欲求角 表示为已知角
表示为已知角 ,解题注意点是开方时根据范围对正负进行取舍.
,解题注意点是开方时根据范围对正负进行取舍. ,∴
,∴ . 1分
. 1分 ,故
,故 ,∴
,∴ .
.  ,解得
,解得 ,
, ,∴
,∴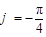 , 4分
, 4分 . 5分
. 5分 的单调增区间为
的单调增区间为 . 8分
. 8分 ,即
,即 ,
, , ∴
, ∴ ,
, , 10分
, 10分

 ,
, . 13分
. 13分

科目:高中数学 来源:不详 题型:解答题
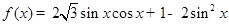 ,xÎR.
,xÎR.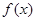 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;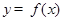 的图象上各点的纵坐标保持不变,横坐标先缩短到原来的
的图象上各点的纵坐标保持不变,横坐标先缩短到原来的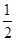 ,把所得到的图象再向左平移
,把所得到的图象再向左平移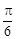 单位,得到函数
单位,得到函数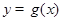 的图象,求函数
的图象,求函数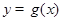 在区间
在区间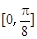 上的最小值.
上的最小值. 查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
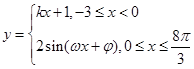 ,的图像如图所示,则函数
,的图像如图所示,则函数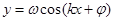 ,
,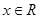 的图像纵坐标不变,横坐标缩短到原来的
的图像纵坐标不变,横坐标缩短到原来的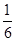 ,再向左平移
,再向左平移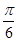 个单位后,得到y=g(x)的图像,则函数
个单位后,得到y=g(x)的图像,则函数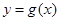 在(0,
在(0,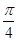 )上( )
)上( )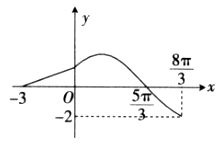
| A.是减函数 | B.是增函数 | C.先增后减函数 | D.先减后增函数 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 sin ωx·cos ωx+cos 2ωx-
sin ωx·cos ωx+cos 2ωx- (ω>0),其最小正周期为
(ω>0),其最小正周期为 .
. 个单位,再将图象上各点的横坐标伸长到原来的2倍(纵坐标不变),得到函数y=g(x)的图象,若关于x的方程g(x)+k=0,在区间
个单位,再将图象上各点的横坐标伸长到原来的2倍(纵坐标不变),得到函数y=g(x)的图象,若关于x的方程g(x)+k=0,在区间 上有且只有一个实数解,求实数k的取值范围.
上有且只有一个实数解,求实数k的取值范围.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com