
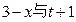 �ɷ����������������������ױƷ��������ֻ����1�������֪2010��������ױƷ���豸�۾ɡ�ά�ȹ̶�����Ϊ3��Ԫ��ÿ����1�����ױƷ��Ҫ��Ͷ��32��Ԫ���������ã�����ÿ����ױƷ���ۼ۶�Ϊ���������ɱ���150%��ƽ��ÿ�������ѵ�һ��֮�ͣ����������Ļ�ױƷ���������ꡣ
�ɷ����������������������ױƷ��������ֻ����1�������֪2010��������ױƷ���豸�۾ɡ�ά�ȹ̶�����Ϊ3��Ԫ��ÿ����1�����ױƷ��Ҫ��Ͷ��32��Ԫ���������ã�����ÿ����ױƷ���ۼ۶�Ϊ���������ɱ���150%��ƽ��ÿ�������ѵ�һ��֮�ͣ����������Ļ�ױƷ���������ꡣ ��2��
��2��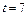
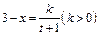 ����������������������������������1��
����������������������������������1��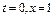 ����ã�
����ã�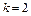 ��������������������������������������2��
��������������������������������������2��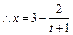 ��������������������������������3��
��������������������������������3��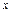 �������ʱ
�������ʱ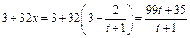
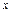 �������ʱ������������=
�������ʱ������������= ��
��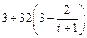 ��+
��+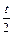 =
=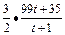 +
+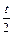
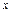 �����ױƷ�������꣬
�����ױƷ�������꣬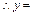
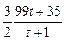 +
+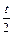 ��
��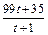 ��
��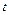
 ��������������������������������6��
��������������������������������6�� ��������������������������������9��
��������������������������������9��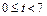 ʱ��
ʱ��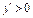 ����
����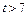 ʱ
ʱ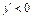 .
.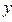 ��
��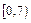 �ϵ�����������
�ϵ�����������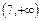 �ϵ����ݼ�. ��������������������11��
�ϵ����ݼ�. ��������������������11��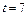 ʱ��
ʱ��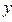 ȡ���ֵ.
ȡ���ֵ.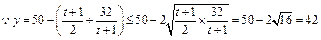 ������������������������10��
������������������������10��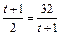 ʱȡ�Ⱥ�.��t=7ʱ��
ʱȡ�Ⱥ�.��t=7ʱ��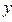 ȡ���ֵ. ����������������
ȡ���ֵ. ���������������� ������11��
������11��


| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ ���ͣ������
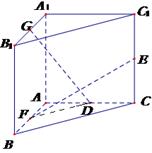
 ��ͼ������N��1��n��Ϊ�е�����ߵ���б��Ϊ
��ͼ������N��1��n��Ϊ�е�����ߵ���б��Ϊ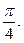
 ��2���Ƿ������С��������k��ʹ�ò���ʽ
��2���Ƿ������С��������k��ʹ�ò���ʽ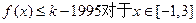 �������������ڣ��������С��������k����������ڣ���˵�����ɣ�
�������������ڣ��������С��������k����������ڣ���˵�����ɣ� ����֤��
����֤��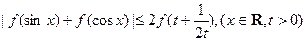 .
.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
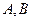 ���صľ�����120km���������͵ļ۸���6Ԫ/������
���صľ�����120km���������͵ļ۸���6Ԫ/������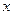 km/h������
km/h������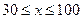 ���ٶ���ʻʱ�������ĺ�����Ϊ
���ٶ���ʻʱ�������ĺ�����Ϊ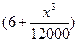 L/h��˾��ÿСʱ�Ĺ�����28Ԫ����ô��õij����Ƕ��٣��粻�����������ã�����г����ܷ����Ƕ��٣�
L/h��˾��ÿСʱ�Ĺ�����28Ԫ����ô��õij����Ƕ��٣��粻�����������ã�����г����ܷ����Ƕ��٣��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
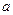
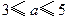
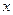
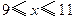
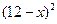
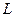 ����Ԫ����ÿ����Ʒ���ۼ�
����Ԫ����ÿ����Ʒ���ۼ�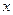 �ĺ�����ϵʽ��
�ĺ�����ϵʽ��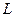 �����
����� ��
��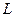 �����ֵ
�����ֵ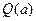
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��
 ���� �� ��
���� �� ��A�� �� �� ���Ǽ����� ���Ǽ����� | B�� �� �� ���������� ���������� |
C�� �� �� ���Ǽ����� ���Ǽ����� | D�� �� �� ���������� ���������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
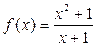
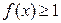 ��
��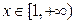 ʱ������
ʱ������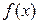 ����Сֵ��
����Сֵ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
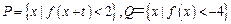 ��
�� �ij�ֲ���Ҫ��������ʵ��
�ij�ֲ���Ҫ��������ʵ��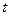 ��ȡֵ��Χ�� ��
��ȡֵ��Χ�� ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��
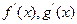 �ֱ���f(x)��g(x)�ĵ���������
�ֱ���f(x)��g(x)�ĵ���������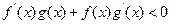 ����
����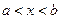 ʱ���У� ��
ʱ���У� ��| A��f(x)g(x)>f(b)g(b) | B��f(x)g(a)>f(a)g(x) |
| C��f(x)g(b)>f(b)g(x) | D��f(x)g(x)>f(a) g(a) g(a) |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��
| A��20.6 | B��21 | C��22 | D��23 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com