
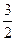 )是椭圆E:
)是椭圆E: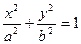 (
(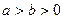 )上一点,F1、F2分别是椭圆E的左、右焦点,O是坐标原点,PF1⊥x轴.
)上一点,F1、F2分别是椭圆E的左、右焦点,O是坐标原点,PF1⊥x轴.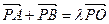 (0<λ<4,且λ≠2).求证:直线AB的斜率等于椭圆E的离心率;
(0<λ<4,且λ≠2).求证:直线AB的斜率等于椭圆E的离心率; x轴,
x轴,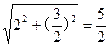 ,2a=|PF1|+|PF2|=4,a=2,b2=3,
,2a=|PF1|+|PF2|=4,a=2,b2=3,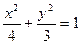 ;…………………3分
;…………………3分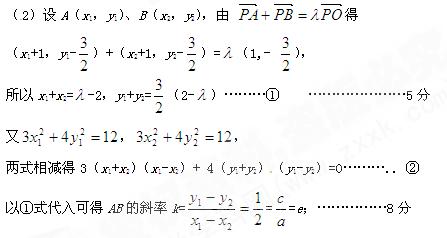
 x+t,
x+t,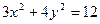 联立消去y并整理得 x2+tx+t2-3=0,
联立消去y并整理得 x2+tx+t2-3=0,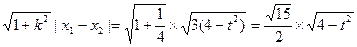 ,
,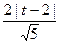 ,
, 积为S
积为S =
=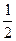 |AB|×d=
|AB|×d=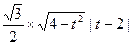 , ………10分
, ………10分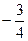 (t4-4t3+16t-16) (-2<t<2),
(t4-4t3+16t-16) (-2<t<2),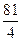 ,
,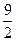 .
.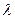 -2,
-2,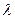 =3.……………………………………12分
=3.……………………………………12分

 备战中考寒假系列答案
备战中考寒假系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com