
| 年龄/周岁 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 身高/cm | 90.8 | 97.6 | 104.2 | 110.9 | 115.6 | 122.0 | 128.5 |
| 年龄/周岁 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 身高/cm | 134.2 | 140.8 | 147.6 | 154.2 | 160.9 | 167.6 | 173.0 |
科目:高中数学 来源:不详 题型:解答题
 与
与 ,其观测值的
,其观测值的 列联表如下:
列联表如下: |  |  合计 合计 | |
 |  |  |  |
 |  | 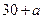 | 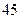 |
| 合计 |  |  |  |
 ,
, 均为大于
均为大于 的整数,若
的整数,若 时,有
时,有 的把握认为两个分类变量
的把握认为两个分类变量 与
与 有关系,那么
有关系,那么 为何值时,我们有
为何值时,我们有 的把握认为两个分类变量
的把握认为两个分类变量 与
与 有关系?
有关系?查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| | 理科 | 文科 |
| 男 | 13 | 10 |
| 女 | 7 | 20 |
 .根据表中数据,得到
.根据表中数据,得到 , 则认为选修文科与性别有关系出错的可能性是( )
, 则认为选修文科与性别有关系出错的可能性是( )查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 年 份 | 1993 | 1994 | 1995 | 1996 | 1997 | 1998 | 1999 | 2000 | 2001 | 2002 |
| x用户(万户) | 1 | 1.2 | 1.6 | 1.8 | 2 | 2.5 | 3.2 | 4 | 4.2 | 4.5 |
| y (百万立米) | 6 | 7 | 9.8 | 12 | 12.1 | 14.5 | 20 | 24 | 25.4 | 27.5 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| | 焦虑 | 说谎 | 懒惰 | 总计 |
| 女生 | 5 | 10 | 15 | 30 |
| 男生 | 20 | 10 | 50 | 80 |
| 总计 | 25 | 20 | 65 | 110 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| x | 0 | 1 | 2 | 3 |
| y | 1 | 3 | 5 | 7 |
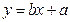 必过( )
必过( )| A.(2,2)点 | B.(1.5,0)点 | C.(1,2)点 | D.(1.5,4)点 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 | 文艺节目 | 新闻节目 | 总计 |
| 大于40岁 | 40 | 30 | 70 |
| 20至40岁 | 160 | 270 | 430 |
| 总计 | 200 | 300 | 500 |
| A.有99%的把握认为收看不同节目类型的观众 与年龄有关 |
| B.有95%的把握认为收看不同节目类型的观众 与年龄有关 |
| C.有99%的把握认为收看不同节目类型的观众 与年龄无关 |
| D.有95%的把握认为收看不同节目类型的观众 与年龄无关 |
 )
)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com