
在△ABC中,角A,B,C的对边分别为a,b,c.已知2cos(B-C)+1=4cosBcosC.
(Ⅰ)求A;
(Ⅱ)若a=2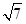 ,△ABC的面积为2
,△ABC的面积为2 ,求b+c.
,求b+c.
(Ⅰ)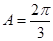 ;(Ⅱ)6.
;(Ⅱ)6.
解析试题分析:(Ⅰ) 对于2cos(B-C)+1=4cosBcosC通过三角恒等变换,再结合角的范围即可得;(Ⅱ)利用余弦定理、面积公式可求.
试题解析:(Ⅰ) 由2cos(B-C)+1=4cosBcosC,得
2(cosBcosC+sinBsinC)+1=4cosBcosC,
即2(cosBcosC-sinBsinC)=1,亦即2cos(B+C)=1,
∴cos(B+C)=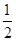 . ∵0<B+C<π,∴B+C=
. ∵0<B+C<π,∴B+C=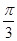 .
.
∵A+B+C=π, ∴A=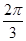 . 6分
. 6分
(Ⅱ)由(Ⅰ),得A=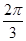 .
.
由S△ABC=2 ,得
,得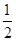 bcsin
bcsin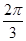 =2
=2 ,∴bc=8. ①
,∴bc=8. ①
由余弦定理a2=b2+c2-2bccosA,得
(2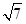 )2=b2+c2-2bccos
)2=b2+c2-2bccos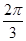 ,即b2+c2+bc=28,
,即b2+c2+bc=28,
∴(b+c)2-bc=28. ②
将①代入②,得(b+c)2-8=28,
∴b+c=6. 12分
考点:解三角形,正、余弦定理,面积公式


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
已知点 D 为ΔABC 的边 BC 上一点.且 BD ="2DC," 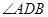 =750,
=750,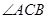 ="30°,AD" =
="30°,AD" =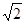 .
.
(I)求CD的长;
(II)求ΔABC的面积
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为了测量两山顶M,N间的距离,飞机沿水平方向在A,B两点进行测量,A,B,M,N在同一个铅垂平面内(如示意图),飞机能够测量的数据有俯角和A,B间的距离,请设计一个方案,包括:①指出需要测量的数据(用字母表示,并在图中标出);②用文字和公式写出计算M,N间的距离的步骤。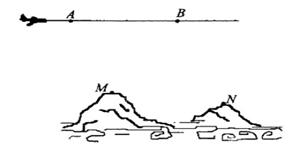
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com