
当x>0时,下列函数中最小值为2的是
A.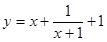 B.
B.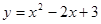
C. D.
D.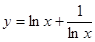
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
.设函数y=f(x)的定义域为(0,+∞),且对任意的正实数x, y,均有
f(xy)=f(x)+f(y)恒成立.已知f(2)=1,且当x>1时,f(x)>0。
(1)求f(1), f(![]() )的值;
)的值;
(2)试判断y=f(x)在(0,+∞)上的单调性,并加以证明;
(3)一个各项均为正数的数列{a??n}满足f(Sn)=f(an)+f(an+1)-1,n∈N*,其中Sn是数列{an}的前n项和,求数列{an}的通项公式;
(4)在(3)的条件下,是否存在正数M,使2n·a1·a2…an≥M·![]() .(2a1-1)·(2a2-1)…(2an-1)对于一切n∈N*均成立?若存在,求出M的范围;若不存在,请说明理由.
.(2a1-1)·(2a2-1)…(2an-1)对于一切n∈N*均成立?若存在,求出M的范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2009-2010学年度新课标高三下学期数学单元测试3-文科 题型:解答题
(2010届枣庄市第一次调研)
已知函数f(x)对任意的实数x、y都有f(x+y) =f(x)+f(y)-1,且当x>0 时,f(x)>1.
(1)求证:函数f(x)在R上是增函数;
(2)若关于x的不等式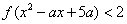 的解集为{x|-3<x<2=,求f(2009)的值;
的解集为{x|-3<x<2=,求f(2009)的值;
(3)在(2)的条件下,设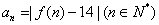 ,若数列
,若数列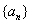 从第k项开始的连续20项 之和等于102,求k的值.
从第k项开始的连续20项 之和等于102,求k的值.
查看答案和解析>>
科目:高中数学 来源:2009-2010学年度新课标高三下学期数学单元测试3-理科 题型:解答题
已知函数f(x)对任意的实数x、y都有f(x+y) =f(x)+f(y)-1,且当x>0 时,
f(x)>1.
(1)求证:函数f(x)在R上是增函数;
(2)若关于x的不等式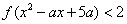 的解集为{x|-3<x<2=,求f(2009)的值;
的解集为{x|-3<x<2=,求f(2009)的值;
(3)在(2)的条件下,设 ,若数列
,若数列 从第k项开始的连续20项之和等于102,求k的值.
从第k项开始的连续20项之和等于102,求k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
|
已知定义域为R的函数f(x)满足f(-x)= -f(x+4),当x>2时,f(x)单调递增,如果x1+x2<4且(x1-2)(x2-2)<0,则f(x1)+f(x2)的值 ( ) A.恒小于0 B.恒大于0 C.可能为0 D.可正可负 查看答案和解析>> 科目:高中数学 来源: 题型: 吉林省吉林一中2011届高三下学期冲刺试题一(数学理).doc | | |
|