Question

在等差数列{a_n}中，a₁+a₂+a₃=3，a₂₈+a₂₉+a₃₀=165，则此数列前30项和等于________．

Answer 1

840
分析：在等差数列{a_n}中，由a₁+a₂+a₃=3，a₂₈+a₂₉+a₃₀=165，知a₂+a₂₉=56，再由
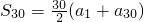
=15（a₂+a₂₉），能求出此数列前30项和．
解答：在等差数列{a_n}中，
∵a₁+a₂+a₃=3，a₂₈+a₂₉+a₃₀=165，
∴，
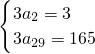
解得a₂+a₂₉=56，
∴此数列前30项和：

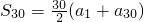
=15（a₂+a₂₉）
=15×56
=840．
故答案为：840．
点评：本题考查等差数列的前n项公式和通项公式，是中档题．解题时要认真审题，仔细解答，注意合理地进行等价转化．