
分析 (1)设直线AB的方程为y=k(x-1)+3,代入3x2+y2=λ,整理得:(k2+3)x2-2k(k-3)x+(k-3)2-λ=0,然后结合题设条件由根与经数的关系和根的判别式能够求出直线AB的方程.
(2)由题意知直线CD的方程为x-y+2=0代入椭圆方程,整理得4x2+4x+4-λ=0.由弦长公式可得|CD|.将直线AB的方程x+y-4=0代入椭圆方程得4x2-8x+16-λ=0.同理可得|AB|.由此可以推出存在这样的λ,使得A、B、C、D四点在同一个圆上.
解答 解:(1)依题意,可设直线AB的方程为y=k(x-1)+3,
代入3x2+y2=λ,整理得:(k2+3)x2-2k(k-3)x+(k-3)2-λ=0,①
设A(x1,y1),B(x2,y2),则x1,x2是方程①的两个不同的根,
∴△=4[λ(k2+3)-3(k-3)2]>0,②
且x1+x2=$\frac{2k(k-3)}{k+3}$.
由N(1,3)是线段AB的中点,得x1+x2=2,
∴k(k-3)=k2+3解得k=-1,代入②得λ>12,
即λ的取值范围是(12,+∞).
于是直线AB的方程为y-3=-(x-1),即x+y-4=0.
(2)∵CD垂直平分AB,
∴直线CD的方程为y-3=x-1,即x-y+2=0代入椭圆方程,整理得4x2+4x+4-λ=0.③
又设C(x3,y3),D(x4,y4),CD的中点为M(x0,y0),
则x3,x4是方程③的两根,
∴x3+x4=-1,且x0=$\frac{{x}_{3}+{x}_{4}}{2}$=-$\frac{1}{2}$,y0=x0+2=$\frac{3}{2}$,即M(-$\frac{1}{2}$,$\frac{3}{2}$)
于是由弦长公式可得|CD|=$\sqrt{1+\frac{1}{{k}^{2}}}$•|x3-x4|=$\sqrt{2(λ-3)}$.④
将直线AB的方程x+y-4=0代入椭圆方程得4x2-8x+16-λ=0.⑤
同理可得|AB|=$\sqrt{1+{k}^{2}}$•|x1-x2|=$\sqrt{2(λ-12)}$.⑥
∵当λ>12时,$\sqrt{2(λ-3)}$>$\sqrt{2(λ-12)}$,
∴|AB|<|CD|.
假设存在λ>12,使得A、B、C、D四点共圆,则CD必为圆的直径,点M为圆心.
点M到直线AB的距离为d=$\frac{|-\frac{1}{2}+\frac{3}{2}-4|}{\sqrt{2}}$=$\frac{3\sqrt{2}}{2}$.⑦
于是,由④⑥⑦式及勾股定理可得|MA|2=|MB|2=d2+$|\frac{AB}{2}{|}^{2}$=$\frac{λ-3}{2}$=$|\frac{CD}{2}{|}^{2}$.
故当λ>12时,A、B、C、D四点均在以M为圆心,|$\frac{CD}{2}$|为半径的圆上.
点评 本题综合考查直线和椭圆的位置关系,考查圆的方程,考查学生分析解决问题的能力,难度较大,


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
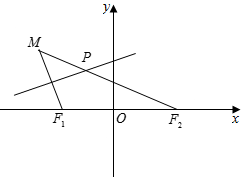 如图所示,点F1(-$\sqrt{3}$,0),F2($\sqrt{3}$,0),动点M到点F2的距离是2$\sqrt{6}$,线段MF1的中垂线交MF2于点P.
如图所示,点F1(-$\sqrt{3}$,0),F2($\sqrt{3}$,0),动点M到点F2的距离是2$\sqrt{6}$,线段MF1的中垂线交MF2于点P.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | P4<1=P1=P2<P3=2 | B. | P1<1=P4=P2<P3=2 | C. | P4=1=P1=P2<P3=2 | D. | P4=1=P1<P2<P3=2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2:1 | B. | 4:1 | C. | 8:1 | D. | 16:1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1.70.2>0.73 | B. | lg3.4<lg2.9 | ||
| C. | log0.31.8<log0.32.7 | D. | 1.72>1.73 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com