Question

15．已知：矩形A₁ABB₁，且AB=2AA₁，C₁，C分别是A₁B₁、AB的中点，D为C₁C中点，将矩形A₁ABB₁沿着直线C₁C折成一个60°的二面角，如图所示．

（Ⅰ）求证：AB₁⊥A₁D；
（Ⅱ）求AB₁与平面A₁B₁D所成角的正弦值．．

Answer 1

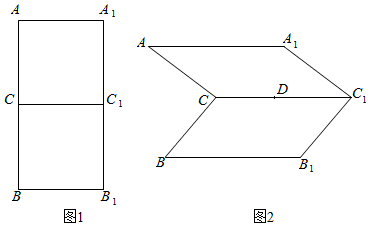
分析 （I）连结AB、A₁B₁，则可证明几何体ABC-A₁B₁C₁是正三棱柱．取BC中点O，B₁C₁的中点O₁，连结OA，OO₁，以O为原点建立坐标系，设AA₁=2，求出$\overrightarrow{A{B}_{1}}$和$\overrightarrow{{A}_{1}D}$的坐标，通过计算$\overrightarrow{A{B}_{1}}•\overrightarrow{{A}_{1}D}=0$得出AB₁⊥A₁D；
（II）求出平面A₁B₁D的法向量$\overrightarrow{n}$，则AB₁与平面A₁B₁D所成角的正弦值为|cos＜$\overrightarrow{n}，\overrightarrow{A{B}_{1}}$＞|．

解答 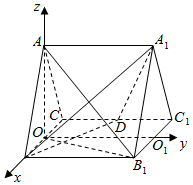证明：（Ⅰ）连结AB、A₁B₁，
∵C₁，C分别是矩形A₁ABB₁边A₁B₁、AB的中点，
∴AC⊥CC₁，BC⊥CC₁，AC∩BC=
∴CC₁⊥面ABC
∴∠ACB为二面角A-CC'-A'的平面角，则∠ACB=60°．
∴△ABC为正三角形，即几何体ABC-A₁B₁C₁是正三棱柱．
取BC中点O，B₁C₁的中点O₁，连结OA，OO₁，则OA⊥平面BB₁C₁C，OO₁⊥BC．
以O为原点，以OB，OO₁，OA的方向为x，y，z轴的正方向建立空间直角坐标系，
不妨设AA₁=2，则A（0，0，$\sqrt{3}$），B₁（1，2，0），D（-1，1，0），A₁（0，2，$\sqrt{3}$）．
∴$\overrightarrow{A{B}_{1}}$=（1，2，-$\sqrt{3}$），$\overrightarrow{{A_1}D}=（-1，-1，-\sqrt{3}）$，
∴$\overrightarrow{A{B}_{1}}•\overrightarrow{{A}_{1}D}$=1×（-1）+2×（-1）+（-$\sqrt{3}$）×（-$\sqrt{3}$）=0，
∴$\overrightarrow{A{B_1}}⊥\overrightarrow{{A_1}D}$
∴AB₁⊥A₁D．
（Ⅱ）$\overrightarrow{{A}_{1}{B}_{1}}$=（1，0，-$\sqrt{3}$），
设平面A₁B₁D的法向量为$\overrightarrow{n}$=（x，y，z）．则$\overrightarrow n⊥\overrightarrow{{A_1}{B_1}}$，$\overrightarrow n⊥\overrightarrow{{A_1}D}$．
∴$\left\{\begin{array}{l}x-\sqrt{3}z=0\\-x-y-\sqrt{3}z=0\end{array}\right.$，令z=1，得$\overrightarrow n=（\sqrt{3}，-2\sqrt{3}，1）$．
∴cos＜$\overrightarrow{n}，\overrightarrow{A{B}_{1}}$＞=$\frac{\overrightarrow{n}•\overrightarrow{A{B}_{1}}}{|\overrightarrow{n}||\overrightarrow{A{B}_{1}}|}$=$\frac{-4\sqrt{3}}{4•2\sqrt{2}}$=-$\frac{{\sqrt{6}}}{4}$．
∴AB₁与平面A₁B₁D所成角的正弦值为$\frac{{\sqrt{6}}}{4}$．

点评 本题考查了空间向量在立体几何中的应用，线面角的计算，属于中档题．