
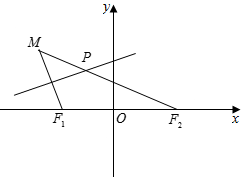
 如图所示,点F1(-$\sqrt{3}$,0),F2($\sqrt{3}$,0),动点M到点F2的距离是2$\sqrt{6}$,线段MF1的中垂线交MF2于点P.
如图所示,点F1(-$\sqrt{3}$,0),F2($\sqrt{3}$,0),动点M到点F2的距离是2$\sqrt{6}$,线段MF1的中垂线交MF2于点P.分析 (I)据题意,动点P的轨迹是以点F1(-$\sqrt{3}$,0),F2($\sqrt{3}$,0)为焦点的抛物线,且a=$\sqrt{6}$,c=$\sqrt{3}$,即可得到椭圆方程;
(Ⅱ)据题意,四边形OASB为矩形即$\overrightarrow{OA}•\overrightarrow{OB}$=0,即x1x2+y1y2=0.设出直线方程,将直线方程与椭圆方程联立,据韦达定理表示出则x1x2+y1y2=0,解方程求出参数,即得到直线方程.
解答 解:(I)由题意|PF1|+|PF2|=|MF2|=2$\sqrt{6}$>|F1F2|,
∴动点P的轨迹是以点F1(-$\sqrt{3}$,0),F2($\sqrt{3}$,0)为焦点的抛物线,且a=$\sqrt{6}$,c=$\sqrt{3}$
∴b2=a2-c2=3,
∴椭圆方程为:$\frac{{x}^{2}}{6}+\frac{{y}^{2}}{3}$=1;
(Ⅱ)因为$\overrightarrow{OS}$=$\overrightarrow{OA}$+$\overrightarrow{OB}$,所以四边形OASB为平行四边形
若存在l使得|OS|=|AB|,则四边形OASB为矩形,∴$\overrightarrow{OA}•\overrightarrow{OB}$=0
若l的斜率不存在,直线l的方程为x=2,则A(2,1),B(2,-1)
∴$\overrightarrow{OA}•\overrightarrow{OB}$=3与$\overrightarrow{OA}•\overrightarrow{OB}$=0矛盾,故l的斜率存在.
设l的方程为y=k(x-2),A(x1,y1),B(x2,y2),
代入椭圆方程可得(2k2+1)x2-8k2x+8k2-6=0,
∴x1+x2=$\frac{8{k}^{2}}{2{k}^{2}+1}$,x1x2=$\frac{8{k}^{2}-6}{2{k}^{2}+1}$,
∴y1y2=k(x1-2)•k(x2-2)=-$\frac{2{k}^{2}}{2{k}^{2}+1}$
∴$\overrightarrow{OA}•\overrightarrow{OB}$=x1x2+y1y2=$\frac{8{k}^{2}-6}{2{k}^{2}+1}$-$\frac{2{k}^{2}}{2{k}^{2}+1}$=0,
∴k=±1
∴存在直线x-y-2=0或x+y-2=0使得四边形OASB的对角线相等
点评 本题考查椭圆方程的求法;考查直线与椭圆的位置关系,解决的关键是将已知转化为x1x2+y1y2=0,属于一道中档题.


 优生乐园系列答案
优生乐园系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 太极图是由黑白两个鱼形纹组成的图案,俗称阴阳鱼,太极图展现了一种互相转化,相对统一的和谐美.定义:能够将圆O的周长和面积同时等分成两个部分的函数称为圆O的一个“太极函数”.则下列有关说法中:
太极图是由黑白两个鱼形纹组成的图案,俗称阴阳鱼,太极图展现了一种互相转化,相对统一的和谐美.定义:能够将圆O的周长和面积同时等分成两个部分的函数称为圆O的一个“太极函数”.则下列有关说法中:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
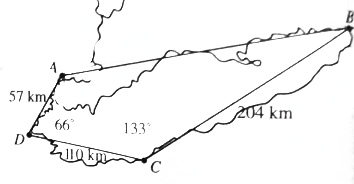 如图,一架飞机以326km/h的速度,沿北偏东75°的航向从城市A出发向城市B飞行,18min以后,飞机由于天气原因按命令改飞另一个城市C,问收到命令时飞机应该沿什么航向飞行,此时离城市C的距离是多少?
如图,一架飞机以326km/h的速度,沿北偏东75°的航向从城市A出发向城市B飞行,18min以后,飞机由于天气原因按命令改飞另一个城市C,问收到命令时飞机应该沿什么航向飞行,此时离城市C的距离是多少?查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1}{3}$,$\frac{1}{3}$,$\frac{1}{3}$) | B. | ($\frac{1}{3}$,$\frac{1}{3}$,$\frac{1}{6}$) | C. | ($\frac{1}{3}$,$\frac{1}{6}$,$\frac{1}{3}$) | D. | ($\frac{1}{6}$,$\frac{1}{3}$,$\frac{1}{3}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com