
 太极图是由黑白两个鱼形纹组成的图案,俗称阴阳鱼,太极图展现了一种互相转化,相对统一的和谐美.定义:能够将圆O的周长和面积同时等分成两个部分的函数称为圆O的一个“太极函数”.则下列有关说法中:
太极图是由黑白两个鱼形纹组成的图案,俗称阴阳鱼,太极图展现了一种互相转化,相对统一的和谐美.定义:能够将圆O的周长和面积同时等分成两个部分的函数称为圆O的一个“太极函数”.则下列有关说法中:分析 利用新定义逐个判断函数是否满足新定义即可.
解答 解:对①显然错误,如图
对②,点(0,1)均为两曲线的对称中心,且f(x)=sinx+1能把圆一分为二,正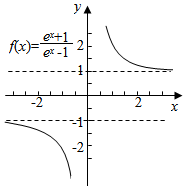
对③,函数为奇函数f(x)=$\frac{{e}^{x}+1}{{e}^{x}-1}$=1+$\frac{2}{{e}^{x}-1}$,当x→0(x>0)时,
f(x)→+∞,
当x→+∞时,f(x)→1,[f(x)>1],函数递减;
当x→0(x<0)时,f(x)→-∞,
当x→-∞时,f(x)→-1,[f(x)<-1],
函数f(x)关于(0,0)中心对称,有三条渐近线y=±1,x=0,
可知,函数的对称中心为间断点,故不存在圆使得满足题干条件.
对于④直线(m+1)x-(2m+1)y-1=0恒过定点(2,1),满足题意.
对于⑤函数f(x)=kx3-kx为奇函数,与圆的交点恒坐标为(-1,1),
∴$\left\{\begin{array}{l}{y=k{x}^{3}-kx}\\{{x}^{2}+{y}^{2}=1}\end{array}\right.$,
∴k2x6-2k2x4+(1+k2)x2-1=0,
令t=x2,得k2t3-2k2t2+(1+k2)t-1=0,
即(t-1)(k2t2-k2t2+1)=0
得t=1即x=±1;
对k2t2-k2t2+1,当k=0时显然无解,△<0即0<k2<4时也无解,
即k∈(-2,2)时两曲线仅有两个交点,函数能把圆一分为二,且周长和面积均等分.
若k=±2时,函数图象与圆有4个交点,
若k2>4时,函数图象与圆有6个交点,均不能把圆一分为二.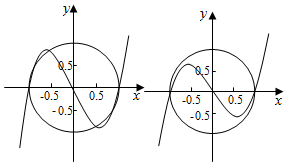 ,
,
故所有正确的是②④⑤
故答案为:②④⑤
点评 本题考查函数的奇偶性的应用,命题真假的判断,新定义的应用,考查转化思想以及计算能力.


 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
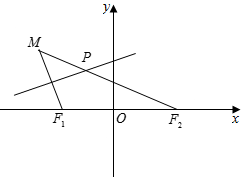 如图所示,点F1(-$\sqrt{3}$,0),F2($\sqrt{3}$,0),动点M到点F2的距离是2$\sqrt{6}$,线段MF1的中垂线交MF2于点P.
如图所示,点F1(-$\sqrt{3}$,0),F2($\sqrt{3}$,0),动点M到点F2的距离是2$\sqrt{6}$,线段MF1的中垂线交MF2于点P.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2:1 | B. | 4:1 | C. | 8:1 | D. | 16:1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com