
分析 分函数f(x)=0无解,有一解,有两解三种情况,分别讨论满足方程f(f(x))=0有两个不等的实数解时,a的取值范围,综合讨论结果,可得答案.
解答 解:①若函数f(x)=x2+2x-a=0无解,
则方程f(f(x))=0也无解;
②若函数f(x)=x2+2x-a=0有两个相等的实数解,
则△=4+4a=0,
解得:a=-1,
f(x)=x2+2x+1≥0恒成立,
∵f(f(x))=0,
∴f(x)=-1,方程无解;
③若函数f(x)=x2+2x-a=0有两个不等的实数解,
则△=4+4a>0,
解得:a>-1,
f(x)=x2+2x-a≥-a-1恒成立,
此时f(x)=0有两根分别为:$-1+\sqrt{a+1}$,$-1-\sqrt{a+1}$
若方程f(f(x))=0有两个不等的实数解,
则$-1-\sqrt{a+1}$<-a-1,且$-1+\sqrt{a+1}$>-a-1,
解得:$\frac{1-\sqrt{5}}{2}$<a<$\frac{1+\sqrt{5}}{2}$,
故答案为:$\frac{1-\sqrt{5}}{2}$<a<$\frac{1+\sqrt{5}}{2}$
点评 本题考查的知识点是二次函数的图象和性质,方程根的个数与函数零点的关系,分类讨论思想,难度中档.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$-$\frac{i}{2}$ | B. | -$\frac{1}{2}$+$\frac{i}{2}$ | C. | $\frac{1}{2}$-$\frac{i}{2}$ | D. | $\frac{1}{2}$+$\frac{i}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30 | B. | 32 | C. | 36 | D. | 48 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 太极图是由黑白两个鱼形纹组成的图案,俗称阴阳鱼,太极图展现了一种互相转化,相对统一的和谐美.定义:能够将圆O的周长和面积同时等分成两个部分的函数称为圆O的一个“太极函数”.则下列有关说法中:
太极图是由黑白两个鱼形纹组成的图案,俗称阴阳鱼,太极图展现了一种互相转化,相对统一的和谐美.定义:能够将圆O的周长和面积同时等分成两个部分的函数称为圆O的一个“太极函数”.则下列有关说法中:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
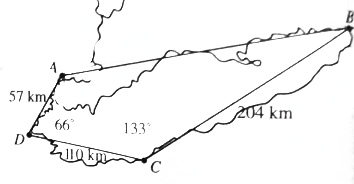 如图,一架飞机以326km/h的速度,沿北偏东75°的航向从城市A出发向城市B飞行,18min以后,飞机由于天气原因按命令改飞另一个城市C,问收到命令时飞机应该沿什么航向飞行,此时离城市C的距离是多少?
如图,一架飞机以326km/h的速度,沿北偏东75°的航向从城市A出发向城市B飞行,18min以后,飞机由于天气原因按命令改飞另一个城市C,问收到命令时飞机应该沿什么航向飞行,此时离城市C的距离是多少?查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com