
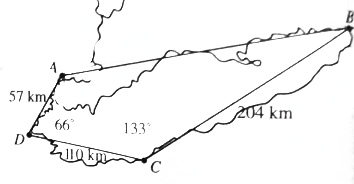
 如图,一架飞机以326km/h的速度,沿北偏东75°的航向从城市A出发向城市B飞行,18min以后,飞机由于天气原因按命令改飞另一个城市C,问收到命令时飞机应该沿什么航向飞行,此时离城市C的距离是多少?
如图,一架飞机以326km/h的速度,沿北偏东75°的航向从城市A出发向城市B飞行,18min以后,飞机由于天气原因按命令改飞另一个城市C,问收到命令时飞机应该沿什么航向飞行,此时离城市C的距离是多少? 分析 设飞机飞到E点时接到命令,连接AC,CE,在△ACD中,根据余弦定理求出AC,正弦定理求出∠ACD,在△ABC中,根据余弦定理,求出AB,∠BAC,在△ACE中,根据余弦定理,求出CE,∠AEC,即可得到所求.
解答 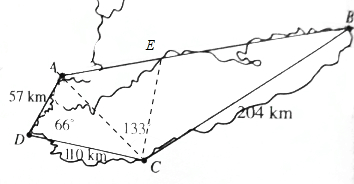 解:设飞机飞到E点时接到命令,
解:设飞机飞到E点时接到命令,
连接AC,CE,
∴AE=$\frac{326×18}{60}$=97.8km,
在△ACD中,根据余弦定理:
AC=$\sqrt{A{D}^{2}+C{D}^{2}-2×AC×CD×cos66°}$
=$\sqrt{5{7}^{2}+11{0}^{2}-2×57×110×cos66°}$
=101.235,
根据正弦定理得,$\frac{AD}{sin∠ACD}$=$\frac{AC}{sin∠ADC}$,
∴sin∠ACD=$\frac{AD×sin∠ADC}{AC}$=$\frac{57×sin66°}{101.235}$=0.5144,
∴∠ACD=30.96°,
∴∠ACB=133°-30.96°=102.04°,
在△ABC中,根据余弦定理,AB=$\sqrt{A{C}^{2}+B{C}^{2}-2×AC×BC×cos∠ACB}$
=$\sqrt{101.23{5}^{2}+20{4}^{2}-2×101.235×204×cos102.04°}$=245.93,
∴cos∠BAC=$\frac{A{B}^{2}+A{C}^{2}-B{C}^{2}}{2×AB×AC}$=$\frac{245.9{3}^{2}+101.23{5}^{2}-20{4}^{2}}{2×245.93×101.235}$=0.5847,
∴∠BAC=54.21°,
在△ACE中,根据余弦定理,
CE=$\sqrt{A{C}^{2}+A{E}^{2}-2×AC×AE×cos∠EAC}$
=$\sqrt{101.23{5}^{2}+97.{8}^{2}-2×101.235×97.8×0.5487}$=90.75,
∴cos∠AEC=$\frac{A{E}^{2}+E{C}^{2}-A{C}^{2}}{2×AE×EC}$=$\frac{97.{8}^{2}+90.7{5}^{2}-101.23{5}^{2}}{2×97.8×90.75}$=0.4254,
∴∠AEC=64.82°,
∴180°-∠AEC-(180°-75°)=75°-64.82°=10.18°
∴飞机应以南偏西10.18°的方向飞行,飞行距离约为90.75km.
答:飞机应以南偏西10.18°的方向飞行,飞行距离约为90.75km.
点评 本题考查利用数学知识解决实际问题,考查正弦、余弦定理的运用,正确运用正弦、余弦定理是关键.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
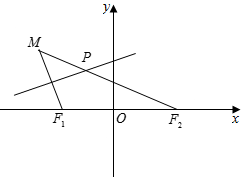 如图所示,点F1(-$\sqrt{3}$,0),F2($\sqrt{3}$,0),动点M到点F2的距离是2$\sqrt{6}$,线段MF1的中垂线交MF2于点P.
如图所示,点F1(-$\sqrt{3}$,0),F2($\sqrt{3}$,0),动点M到点F2的距离是2$\sqrt{6}$,线段MF1的中垂线交MF2于点P.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| t | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| y | 12 | 15.1 | 12.1 | 9.1 | 11.9 | 14.9 | 11.9 | 8.9 | 12.1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2:1 | B. | 4:1 | C. | 8:1 | D. | 16:1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com