
| t | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| y | 12 | 15.1 | 12.1 | 9.1 | 11.9 | 14.9 | 11.9 | 8.9 | 12.1 |
分析 根据最大值和最小值求出A和h,根据相邻的两个最大值之间横坐标的差,求得周期,从而求得ω,再把特殊点代入求得φ的值,从而得到函数的解析式.
解答 解:由图表可得函数y=k+Asin(ωt+φ)的最大值为15,最小值为9,
故k=$\frac{15+9}{2}$=12,且A=15-12=3.
由于当函数取得最大值时,相邻的两个t值分别为t=3和t=15,
故函数的周期等于15-3=12=$\frac{2π}{ω}$,
解得ω=$\frac{π}{6}$,
故函数的解析式为 y=12+3sin($\frac{π}{6}$t+φ).
再由当t=0时,函数值等于12可得=12+3sinφ=12,
∴sinφ=0,
∴φ=kπ,k∈z,故可取φ=0.
故函数的解析式为y=12+3sin($\frac{π}{6}$t),
故答案为:y=12+3sin($\frac{π}{6}$t).
点评 本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,根据最大值和最小值求出A和h,根据相邻的两个最大值之间横坐标的差,求得周期,从而求得ω,再把特殊点代入求得φ的值,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 30 | B. | 32 | C. | 36 | D. | 48 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
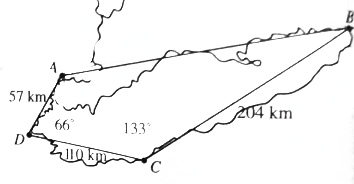 如图,一架飞机以326km/h的速度,沿北偏东75°的航向从城市A出发向城市B飞行,18min以后,飞机由于天气原因按命令改飞另一个城市C,问收到命令时飞机应该沿什么航向飞行,此时离城市C的距离是多少?
如图,一架飞机以326km/h的速度,沿北偏东75°的航向从城市A出发向城市B飞行,18min以后,飞机由于天气原因按命令改飞另一个城市C,问收到命令时飞机应该沿什么航向飞行,此时离城市C的距离是多少?查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | lg2 | B. | lg3 | C. | $lg\sqrt{2}$ | D. | $lg\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-6,+∞) | B. | (-3,+∞) | C. | [-6,1] | D. | (-3,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com