Question

14．下列计算曲线y=cosx（0≤x≤$\frac{3π}{2}$）与坐标轴围成的面积：
（1）${∫}_{0}^{\frac{3π}{2}}$cosxdx，（2）3${∫}_{0}^{\frac{π}{2}}$cosxdx，（3）${∫}_{0}^{\frac{3π}{2}}$|cosx|dx，（4）面积为3．
用的方法或结果正确的是（2）、（3）、（4）．

Answer 1

分析 根据积分和曲边图象的面积关系分别进行判断即可．

解答 解：∵当0≤x≤$\frac{π}{2}$，时，cosx≥0，当$\frac{π}{2}$≤x≤$\frac{3π}{2}$时，cosx≤0，
∴曲线y=cosx（0≤x≤$\frac{3π}{2}$）与坐标轴围成的面积S=${∫}_{0}^{\frac{π}{2}}$cosxdx-${∫}_{\frac{π}{2}}^{\frac{3π}{2}}$cosxdx，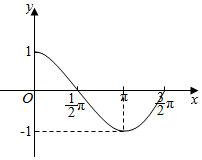
（1）${∫}_{0}^{\frac{3π}{2}}$cosxdx，错误，
（2）函数在0≤x≤$\frac{π}{2}$，$\frac{π}{2}$≤x≤π，π≤x≤$\frac{3π}{2}$三段的面积相同，
则S=3${∫}_{0}^{\frac{π}{2}}$cosxdx，正确
（3）${∫}_{0}^{\frac{3π}{2}}$|cosx|dx，正确
（4）面积为S=3${∫}_{0}^{\frac{π}{2}}$cosxdx=3sinx|${\;}_{0}^{\frac{π}{2}}$=3（sin$\frac{π}{2}$-sin0）=3．
正确，
故答案为：（2）、（3）、（4）；

点评 本题主要考查积分的几何意义，当f（x）≥0时，积分的几何意义为对应曲边图象的面积．