
分析 (1)根据向量数量积的结合三角函数的辅助角公式进行化简求解即可.
(2)根据三角函数的单调性,结合最小值求出a的值即可.
解答 解:(1)f(x)=$\overrightarrow{p}$•$\overrightarrow{q}$-a=2cos2x-2sinxcosx-a=1+cos2x-sin2x-a=$\sqrt{2}$cos(2x+$\frac{π}{4}$)+1-a.(2分)
则f(x)的最小正周期T=$\frac{2π}{2}$=π.(3分)
令-π+2kπ≤2x+$\frac{π}{4}$≤2kπ,k∈Z,解得-$\frac{5π}{8}$+kπ≤x≤-$\frac{π}{8}$+kπ,k∈Z,
故函数f(x)的单调增区间为[-$\frac{5π}{8}$+kπ,-$\frac{π}{8}$+kπ],k∈Z.(5分)
(2)∵x∈[0,$\frac{π}{2}$],
∴2x+$\frac{π}{4}$∈[$\frac{π}{4}$,$\frac{5π}{4}$],则-1≤cos(2x+$\frac{π}{4}$)≤$\frac{\sqrt{2}}{2}$,(7分)
∵f(x)的最小值是-2,
∴当cos(2x+$\frac{π}{4}$)=-1时,函数取得最小值,
此时-$\sqrt{2}$+1-a=-2,则a=3-$\sqrt{2}$,
当cos(2x+$\frac{π}{4}$)=$\frac{\sqrt{2}}{2}$时,函数取得最大值,
此时最大值为f(x)=$\sqrt{2}$×$\frac{\sqrt{2}}{2}$+1-(3-$\sqrt{2}$)=$\sqrt{2}$-1.
点评 本题主要考查向量数量积和三角函数的综合应用,利用辅助角公式以及向量数量积的坐标是进行化简是解决本题的关键.


科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
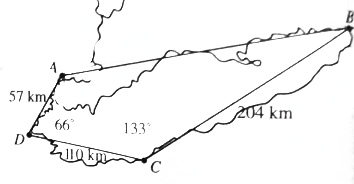 如图,一架飞机以326km/h的速度,沿北偏东75°的航向从城市A出发向城市B飞行,18min以后,飞机由于天气原因按命令改飞另一个城市C,问收到命令时飞机应该沿什么航向飞行,此时离城市C的距离是多少?
如图,一架飞机以326km/h的速度,沿北偏东75°的航向从城市A出发向城市B飞行,18min以后,飞机由于天气原因按命令改飞另一个城市C,问收到命令时飞机应该沿什么航向飞行,此时离城市C的距离是多少?查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-6,+∞) | B. | (-3,+∞) | C. | [-6,1] | D. | (-3,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 存在x>0,使得x2+x≥0 | B. | 存在x>0,使得x2+x<0 | ||
| C. | 任意x≤0,都有x2+x<0 | D. | 任意x≤0,都有x2+x≥0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
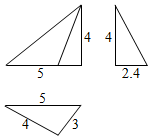
| A. | 16 | B. | 26 | C. | 32 | D. | 20+$\frac{25}{4}\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com