Question

18．已知某几何体的三视图如图所示，则该几何体的表面积为（　　） 

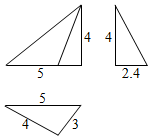
• A． 16
• B． 26
• C． 32
• D． 20+$\frac{25}{4}\sqrt{3}$

Answer 1

分析 几何体是三棱锥，根据三视图可得三棱锥的一侧棱与底面垂直，结合直观图求相关几何量的数据，把数据代入棱锥的表面积公式计算即可．

解答 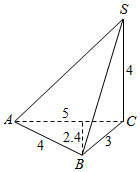解：根据三视图知：该几何体是三棱锥，且三棱锥的一个侧棱与底面垂直，高为4，
如图所示：
其中SC⊥平面ABC，SC=3，AB=4，BC=3，AC=5，SC=4，∴AB⊥BC，
由三垂线定理得：AB⊥BC，
S_△ABC=$\frac{1}{2}$×3×4=6，
S_△SBC=$\frac{1}{2}$×3×4=6，
S_△SAC=$\frac{1}{2}$×4×5=10，
S_△SAB=$\frac{1}{2}$×AB×SB=$\frac{1}{2}$×4×5=10，
∴该几何体的表面积S=6+6+10+10=32．
故选：C．

点评 本题考查了由三视图求几何体的表面积，根据三视图判断几何体的结构特征及求相关几何量的数据是解答本题的关键．