
| A. |  | B. |  | C. |  | D. |  |
分析 当x<0时,函数f(x)=$\frac{1}{x}+ln(-x)$,由函数的单调性,排除CD;
当x>0时,函数f(x)=$\frac{1}{x}+ln(x)$,此时,代入特殊值验证,排除A,只有B正确,
解答 解:当x<0时,函数f(x)=$\frac{1}{x}+ln(-x)$,由函数y=$\frac{1}{x}$、y=ln(-x)递减知函数f(x)=$\frac{1}{x}+ln(-x)$递减,排除CD;
当x>0时,函数f(x)=$\frac{1}{x}+ln(x)$,此时,f(1)=$\frac{1}{1}+ln1$=1,而选项A的最小值为2,故可排除A,只有B正确,
故选:B.
点评 题考查函数的图象,考查同学们对函数基础知识的把握程度以及数形结合与分类讨论的思维能力.


科目:高中数学 来源: 题型:填空题
奖品 收费(元/件) 工厂 | 一等奖奖品 | 二等奖奖品 |
| 甲 | 500 | 400 |
| 乙 | 800 | 600 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2017届云南曲靖市高三上半月考一数学试卷(解析版) 题型:解答题
已知函数 (
( 为自然对数的底数).
为自然对数的底数).
(1)当 时,求过点
时,求过点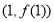 处的切线与坐标轴围成的三角形的面积;
处的切线与坐标轴围成的三角形的面积;
(2)若 在
在 上恒成立,求实数
上恒成立,求实数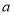 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,过抛物线y2=2px(p>0)的焦点F的直线与抛物线相交于M、N两点,自M、N向准线L作垂线,垂足分别为M1、N1,求证:FM⊥FN.
如图,过抛物线y2=2px(p>0)的焦点F的直线与抛物线相交于M、N两点,自M、N向准线L作垂线,垂足分别为M1、N1,求证:FM⊥FN.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com