
分析 (1)根据函数解析式得出周期为:T=$\frac{2π}{\frac{π}{6}}$=12,f(1)+…+f(12)=0,转化为f(1)+f(2)+f(3)+…f(102)=f(1)+f(2)+…+(6),判断即可.
(2)利用f(6)=0,很容易得出f(1)f(2)f(3)…f(101)=0,
解答 解:(1)∵函数f(n)=sin$\frac{nπ}{6}$(n∈Z),
∴周期为:T=$\frac{2π}{\frac{π}{6}}$=12,
∴f(1)+…+f(12)=0
∴f(1)+f(2)+f(3)+…f(102)=f(1)+f(2)+…+(6)=2+$\sqrt{3}$,
(2)∵f(6)=0,
∴f(1)f(2)f(3)…f(101)=0,
点评 本题考查了三角函数的周期性,利用三角函数的值求解,属于计算题,难度不大.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-3,3] | B. | (-1,3] | C. | (1,3] | D. | (1,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2017届云南曲靖市高三上半月考一数学试卷(解析版) 题型:填空题
已知函数 ,若
,若 是从
是从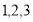 三个数中任取的一个数,
三个数中任取的一个数, 是从
是从 三个数中任取的一个数,则使函数
三个数中任取的一个数,则使函数 有极值点的概率为_______.
有极值点的概率为_______.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com