
分析 (1)由a1=1,且$\frac{{S}_{n}}{{a}_{n}}$=λan+1(n∈N+),分别取n=1,2,可得a2,a3,利用数列{an}的为等差数列,可得2a2=a1+a3,解得λ,再利用通项公式即可得出;
(2)bn=$\frac{1}{{μ}^{{a}_{n}}}$=$\frac{1}{{μ}^{n}}$,可得数列{bn}的前n项和为Tn=$\frac{1}{μ}+\frac{1}{{μ}^{2}}$+…+$\frac{1}{{μ}^{n}}$,判断数列{Tn}是单调性,即可得出.
解答 解:(1)由a1=1,且$\frac{{S}_{n}}{{a}_{n}}$=λan+1(n∈N+),分别取n=1,2,可得a2=$\frac{1}{λ}$,${a}_{3}=1+\frac{1}{λ}$,
∵数列{an}的为等差数列,
∴2a2=a1+a3,
∴$\frac{2}{λ}=1+1+\frac{1}{λ}$,解得λ=$\frac{1}{2}$,
∴d=a2-a1=2-1=1.
∴an=1+(n-1)=n.
(2)bn=$\frac{1}{{μ}^{{a}_{n}}}$=$\frac{1}{{μ}^{n}}$,∴数列{bn}的前n项和为Tn=$\frac{1}{μ}+\frac{1}{{μ}^{2}}$+…+$\frac{1}{{μ}^{n}}$,
∵Tn+1-Tn=$\frac{1}{{μ}^{n+1}}$>0,
∴数列{Tn}是单调递增数列,
∵对任意的n≥2,都有Tn$>\frac{2}{3}$成立,
∴T2=$\frac{1}{μ}$+$\frac{1}{{μ}^{2}}$$>\frac{2}{3}$,又1<μ,解得1<μ<$\frac{3+\sqrt{33}}{4}$,
∴μ的取值范围是$(1,\frac{3+\sqrt{33}}{4})$.
点评 本题考查了等差数列的通项公式、递推式的应用、数列的单调性、一元二次不等式的解法,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
奖品 收费(元/件) 工厂 | 一等奖奖品 | 二等奖奖品 |
| 甲 | 500 | 400 |
| 乙 | 800 | 600 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2017届云南曲靖市高三上半月考一数学试卷(解析版) 题型:解答题
已知函数 (
( 为自然对数的底数).
为自然对数的底数).
(1)当 时,求过点
时,求过点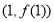 处的切线与坐标轴围成的三角形的面积;
处的切线与坐标轴围成的三角形的面积;
(2)若 在
在 上恒成立,求实数
上恒成立,求实数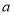 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 18$\sqrt{3}$ | B. | 20$\sqrt{3}$ | C. | 22$\sqrt{3}$ | D. | 24$\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com