
分析 根据增函数的定义,设任意的x1>x2≥1,然后作差,可以看出需要分子有理化,从而可以证明f(x1)>f(x2),这样便可得出f(x)在[1,+∞)上单调递增.
解答 证明:设x1>x2≥1,则:
$f({x}_{1})-f({x}_{2})=\sqrt{{{x}_{1}}^{2}-1}-\sqrt{{{x}_{2}}^{2}-1}$=$\frac{{{x}_{1}}^{2}-{{x}_{2}}^{2}}{\sqrt{{{x}_{1}}^{2}-1}+\sqrt{{{x}_{2}}^{2}-1}}$;
∵x1>x2≥1;
∴${{x}_{1}}^{2}-{{x}_{2}}^{2}>0$,$\sqrt{{{x}_{1}}^{2}-1}+\sqrt{{{x}_{2}}^{2}-1}>0$;
∴f(x1)>f(x2);
∴f(x)在x∈[1,+∞)时单调递增.
点评 考查增函数的定义,以及根据增函数的定义证明一个函数为增函数的方法和过程,作差的方法比较f(x1)与f(x2)的大小,分子有理化的运用.


科目:高中数学 来源: 题型:选择题
| A. | [3,4] | B. | [2,4] | C. | [2,3] | D. | [0,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 梯形 | B. | 矩形但非正方形 | C. | 菱形但非正方形 | D. | 正方形 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
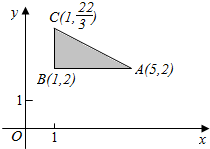 如图所示的坐标平面的可行域内(阴影部分且包括边界),若使目标函数z=ax+y(a>0)取得最大值的最优解有无穷多个,则a的值为( )
如图所示的坐标平面的可行域内(阴影部分且包括边界),若使目标函数z=ax+y(a>0)取得最大值的最优解有无穷多个,则a的值为( )| A. | $\frac{1}{4}$ | B. | $\frac{3}{5}$ | C. | 4 | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1}{2}$,+∞) | B. | (-∞,$\frac{1}{2}$) | C. | (-$\frac{1}{2}$,+∞) | D. | (-∞,-$\frac{1}{2}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com