
(本小题满分12分)在平面直角坐标系 中,直线
中,直线 与抛物线
与抛物线 相交于不同的A、B两点.
相交于不同的A、B两点.
(Ⅰ)如果直线 过抛物线的焦点,求
过抛物线的焦点,求 ·
· 的值;
的值;
(Ⅱ)如果 ·
· =-4,证明直线
=-4,证明直线 必过一定点,并求出该定点.
必过一定点,并求出该定点.
(Ⅰ)-3(Ⅱ)证明略,过定点(2,0)
【解析】
试题分析:解决直线和抛物线的综合问题时注意:第一步:根据题意设直线方程,有的题设条件已知点,而斜率未知;有的题设条件已知斜率,点不定,可由点斜式设直线方程.第二步:联立方程:把所设直线方程与抛物线的方程联立,消去一个元,得到一个一元二次方程.第三步:求解判别式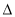 :计算一元二次方程根.第四步:写出根与系数的关系.第五步:根据题设条件求解问题中结论.
:计算一元二次方程根.第四步:写出根与系数的关系.第五步:根据题设条件求解问题中结论.
试题解析:(1)由题意:抛物线焦点为(1,0),设l:x=ty+1,代入抛物线y2=4x,消去x得y2-4ty-4=0,设A(x1,y1),B(x2,y2),则y1+y2=4t,y1y2=-4,
∴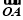 ·
·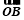 =x1x2+y1y2=(ty1+1)(ty2+1)+y1y2=t2y1y2+t(y1+y2)+1+y1y2=-4t2+4t2+1-4=-3. ----6分
=x1x2+y1y2=(ty1+1)(ty2+1)+y1y2=t2y1y2+t(y1+y2)+1+y1y2=-4t2+4t2+1-4=-3. ----6分
(2)设l:x=ty+b代入抛物线y2=4x,消去x得y2-4ty-4b=0,设A(x1,y1),B(x2,y2),
则y1+y2=4t,y1y2=-4b,
∴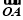 ·
·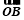 =x1x2+y1y2=(ty1+b)(ty2+b)+y1y2=t2y1y2+bt(y1+y2)+b2+y1y2=-4bt2+4bt2+b2-4b=b2-4b.令b2-4b=-4,∴b2-4b+4=0,∴b=2,∴直线l过定点(2,0).∴若
=x1x2+y1y2=(ty1+b)(ty2+b)+y1y2=t2y1y2+bt(y1+y2)+b2+y1y2=-4bt2+4bt2+b2-4b=b2-4b.令b2-4b=-4,∴b2-4b+4=0,∴b=2,∴直线l过定点(2,0).∴若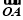 ·
·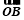 =-4,则直线l必过一定点.
=-4,则直线l必过一定点.
考点:直线与抛物线综合问题.


科目:高中数学 来源:2014-2015学年四川省高二上学期10月月考文科数学卷(解析版) 题型:解答题
(本小题满分12分)已知等比数列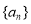 的各项均为正数,且
的各项均为正数,且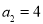 ,
,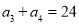 .
.
(1) 求数列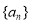 的通项公式;
的通项公式;
(2) 设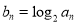 ,求数列
,求数列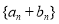 的前
的前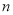 项和
项和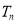 .
.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年四川省成都六校高一上学期期中考试数学试卷(解析版) 题型:选择题
定义区间 的长度均为
的长度均为 ,用
,用 表示不超过
表示不超过 的最大整数,例如
的最大整数,例如 ,
, ,记
,记 ,设
,设 ,若用
,若用 表示不等式
表示不等式 解集区间的长度,则当
解集区间的长度,则当 时有( )
时有( )
A. B.
B. C.
C. D.
D.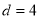
查看答案和解析>>
科目:高中数学 来源:2014-2015学年吉林省高二上学期期初考试理科数学试卷(解析版) 题型:填空题
已知以 为渐近线的双曲线D:
为渐近线的双曲线D: 的左,右焦点分别为F1,F2,若P为双曲线D右支上任意一点,则
的左,右焦点分别为F1,F2,若P为双曲线D右支上任意一点,则 的取值范围是________.
的取值范围是________.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年吉林省高二上学期期初考试理科数学试卷(解析版) 题型:选择题
P是双曲线 上的点,F1,F2是其焦点,双曲线的离心率是
上的点,F1,F2是其焦点,双曲线的离心率是 ,且
,且 ,若△F1PF2的面积是9,则a+b的值等于( )
,若△F1PF2的面积是9,则a+b的值等于( )
A.4 B.5 C.6 D.7
查看答案和解析>>
科目:高中数学 来源:2014-2015学年吉林省高一上学期期初考试数学试卷(解析版) 题型:选择题
若函数y=loga(x2﹣ax+1)有最小值,则a的取值范围是( )
A.0<a<1 B.0<a<2,a≠1 C.1<a<2 D.a≥2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com