
���� ��Ϊf��x���ʦ�1��f��x��∉��2����g��x��=$\frac{f��x��}{x}$=x2-2mx-m�ڣ�0��+�ޣ���������������h��0����h��x��=$\frac{f��x��}{{x}^{2}}$=x-2m-$\frac{m}{x}$�ڣ�0��+�ޣ���������������h�䣨x��=1+$\frac{m}{{x}^{2}}$�����Ե�h��x����������ʱ����h��0�����Ե�h��x������������ʱ����h��0�������������ɵ�h��ȡֵ��Χ�ǣ�-�ޣ�0����
��� �⣺��f��x���ʦ�1��f��x��∉��2��
��g��x��=$\frac{f��x��}{x}$=x2-2mx-m�ڣ�0��+�ޣ�����������
��m��0��
��h��x��=$\frac{f��x��}{{x}^{2}}$=x-2m-$\frac{m}{x}$�ڣ�0��+�ޣ�������������
��h�䣨x��=1+$\frac{m}{{x}^{2}}$��
�൱h��x����������ʱ����m��0��
�൱h��x������������ʱ����m��0��
�����������ɵ�m��ȡֵ��Χ�ǣ�-�ޣ�0����
�ʴ�Ϊ����-�ޣ�0����
���� ���⿼���¶������������ã���Ҫ�����˺����ĵ����ԣ�������Ӧ�ã���һ���е��⣮


 ͬ��������ϰϵ�д�
ͬ��������ϰϵ�д� �ο�ͨ�γ̱�˼ά����������ѵ��ϵ�д�
�ο�ͨ�γ̱�˼ά����������ѵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
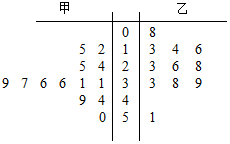 ij�����ף������������˶�Աÿ�������÷ֿ��þ�Ҷͼ��ʾ���£�
ij�����ף������������˶�Աÿ�������÷ֿ��þ�Ҷͼ��ʾ���£��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-�ޣ�2] | B�� | [2��+�ޣ� | C�� | ��-�ޣ�1] | D�� | [1��+��] |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0 | B�� | 1 | C�� | 2 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ʾ��AΪԲO��һ�㣬AO��Բ����B��C���㣬AB=4��ADΪԲO�����ߣ�DΪ�е㣬AD=8����BDC�Ľ�ƽ������BC��ԲO�ֱ���E��F���㣮
��ͼ��ʾ��AΪԲO��һ�㣬AO��Բ����B��C���㣬AB=4��ADΪԲO�����ߣ�DΪ�е㣬AD=8����BDC�Ľ�ƽ������BC��ԲO�ֱ���E��F���㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $��-\frac{1}{3}��+�ޣ�$ | B�� | $[-\frac{1}{3}��+�ޣ�$ | C�� | $��\frac{1}{3}��+�ޣ�$ | D�� | $[\frac{1}{3}��+�ޣ�$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com