
分析 (1)分类讨论,去掉绝对值,即可解不等式f(x)≥2;
(2)已知f(x)是偶函数,f(-x)=f(x),代入计算,即可求a的值.
解答 解:(1)当a=2时f(x)=|x-1|+|x-2|.
由f(x)≥2得|x-1|+|x-2|≥2.
(ⅰ)当x≤1,不等式化为1-x+2-x≥2.即x≤$\frac{1}{2}$.
(ⅱ)当1<x≤2,不等式化为x-1+2-x≥2不可能成立.
(iii)当x>2,不等式化为x-1+x-2≥2,即x≥2.5.
综上得,f(x)≥2的解集为{x|x≤$\frac{1}{2}$或x≥2.5};
(2)∵f(x)是偶函数,
∴f(-x)=f(x),
∴|-x-1|+|-x-a|=|x-1|+|x-a|.
∴a=-1.
点评 本题主要考查绝对值不等式的解法,体现了转化、分类讨论的数学思想,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | [-2,1] | B. | (2,+∞) | C. | (1,2] | D. | (-∞,-2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
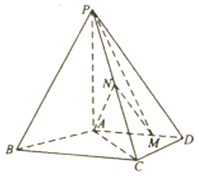 如图,四棱锥P-ABC中,PA⊥平面ABCD,AD∥BC,AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,N为PC的中点.
如图,四棱锥P-ABC中,PA⊥平面ABCD,AD∥BC,AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,N为PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 在一标准大气压下,20℃的纯水结冰 | |
| B. | 平时的百分制考试中,小白的考试成绩为100分 | |
| C. | 抛一枚硬币,落下后正面朝上 | |
| D. | 边长为a,b的长方形面积为ab |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com