
在数列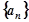 中,已知
中,已知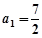 ,
,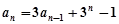 (
(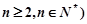 .
.
(1)求证: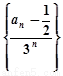 是等差数列;
是等差数列;
(2)求数列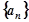 的通项公式
的通项公式 及它的前
及它的前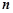 项和
项和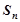 .
.
(1)见解析(2)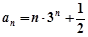 ,
,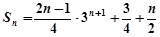
【解析】本试题主要是考查了等差数列的定义以及错位相减法的求和的综合运用。
(1)根据已知的递推关系式,得到数列的相邻两项的关系式,进而结合定义证明。
(2)在第一问的基础上,得到数列的通项公式,然后借助于错位相减法得到结论。
(1)证明:∵ 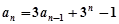 (
(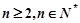 )
)
∴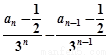
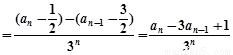
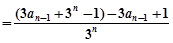
 为常数
为常数
∴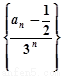 是等差数列,且公差为1.
…………………… 5分
是等差数列,且公差为1.
…………………… 5分
(2)解:由(1)知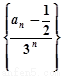 是等差数列,且公差为1,且
是等差数列,且公差为1,且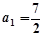
∴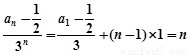 ∴
∴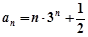 …………… 8分
…………… 8分
∴  ……………
9分
……………
9分
令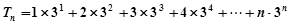 …………①
…………①
则 ……②…………… 10分
……②…………… 10分
两式相减得:
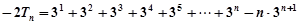 ……………… 11分
……………… 11分

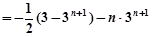 …………… 12分
…………… 12分
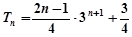 ………………… 13分
………………… 13分
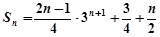 ………………… 14分
………………… 14分


科目:高中数学 来源:2010-2011年四川省成都市玉林中学高一下学期期中考试数学 题型:解答题
((本小题满分14分)
A组.设 是等差数列,
是等差数列, 是各项都为正数的等比数列,且
是各项都为正数的等比数列,且 .
.
(1)求数列 、
、 的通项公式.
的通项公式.
(2)求数列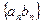 的前
的前 项和
项和
B组.在数列 中,已知:
中,已知: .
.
(1)求证:数列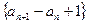 是
是 等比数列.
等比数列.
(2)求数列 的通项公式.
的通项公式.
(3)求和: .
.
查看答案和解析>>
科目:高中数学 来源:2011届河北省唐山一中高三高考仿真理数 题型:解答题
(本小题满分12分)
在数列 中,已知
中,已知 且
且 。
。
(1)记 证明:数列
证明:数列 是等差数列,并求数列
是等差数列,并求数列 的通项公式;
的通项公式;
(2)设 求
求 的值。
的值。
查看答案和解析>>
科目:高中数学 来源:2014届安徽省六校教育研究会高三素质测试文科数学试卷(解析版) 题型:解答题
在数列 中,已知
中,已知 ,
, .
.
(1)求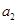 、
、 并判断
并判断 能否为等差或等比数列;
能否为等差或等比数列;
(2)令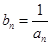 ,求证:
,求证: 为等比数列;
为等比数列;
(3)求数列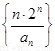 的前n项和
的前n项和 .
.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江西省红色六校高三第二次联考理科数学试卷 题型:解答题
在数列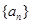 中,已知
中,已知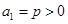 ,且
,且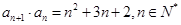 .
.
(1)若数列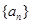 为等差数列,求p的值;
为等差数列,求p的值;
(2)求数列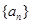 的通项公式;
的通项公式;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com