
分析 (1)由Sn+an=$\frac{1}{2}$(n2+5n+2)(n∈N).利用递推关系即可得出${a}_{n+1}=\frac{1}{2}({a}_{n}+n+3)$.
(2)利用(1)可得a1=2,a2=3,a3=4,…,猜想an=n+1.利用数学归纳法证明即可.
解答 解:(1)由Sn+an=$\frac{1}{2}$(n2+5n+2)(n∈N).令n=1,可得2a1=$\frac{1}{2}×8$,解得a1=2.
当n≥2时,Sn+1+an+1=$\frac{1}{2}[(n+1)^{2}+5(n+1)+2]$,
∴2an+1-an=n+3,
∴${a}_{n+1}=\frac{1}{2}({a}_{n}+n+3)$.
(2)由a1=2,a2=3,a3=4,…,
猜想an=n+1.
下面利用数学归纳法证明:
①当n=1时成立;
②假设当n=k(k∈N*)时,ak=k+1.
则当n=k+1时,ak+1=$\frac{1}{2}(k+1+k+3)$=(k+1)+1.
∴当n=k+1时,假设成立.
综上可得:?n∈N*,an=n+1成立.
点评 本题考查了递推关系、数学归纳法,考查了猜想能力、推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $-\frac{5π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{4π}{3}$ | D. | $\frac{5π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
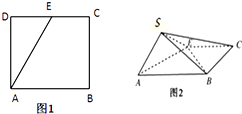 如图,点E为正方形ABCD边CD上异于点C,D的动点,将△ADE沿AE翻折成△SAE,使得平面SAE⊥平面ABCE,则下列三个说法中正确的个数是( )
如图,点E为正方形ABCD边CD上异于点C,D的动点,将△ADE沿AE翻折成△SAE,使得平面SAE⊥平面ABCE,则下列三个说法中正确的个数是( )| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (3,2) | B. | (-3,2) | C. | (-3,-2) | D. | (-2,3) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com