
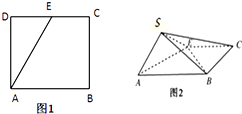
 如图,点E为正方形ABCD边CD上异于点C,D的动点,将△ADE沿AE翻折成△SAE,使得平面SAE⊥平面ABCE,则下列三个说法中正确的个数是( )
如图,点E为正方形ABCD边CD上异于点C,D的动点,将△ADE沿AE翻折成△SAE,使得平面SAE⊥平面ABCE,则下列三个说法中正确的个数是( )| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 根据题意,将△ADE沿AE翻折成△SAE,使平面SAE⊥平面ABCE,可得∠SAD为锐角,判断①错误;
由异面直线的定义可以判断平面SBC内的直线与SA相交或异面,得出②错误;
由线面平行的判定定理,判断出③正确.
解答 解:①当直线SA⊥平面SBC时,BC?平面SBC,∴SA⊥BC;
又AD∥BC,则SA⊥AD,这与∠SAD为锐角矛盾,∴①错误;
②∵平面SBC∩直线SA=S,
∴平面SBC内的直线与SA相交或异面,②错误;
③过点C作CF∥AE,交AB于F,∵CF?平面SAE,AE?平面SAE,
由线面平行的判定定理得,CF∥平面SAE,∴③正确;
综上,正确的命题是③.
故选:B.
点评 本题考查了空间中的平行与垂直的应用问题,也考查了图形折叠问题,是基础题目.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | $\frac{1}{4}$ | C. | 9 | D. | $\frac{1}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\sqrt{3}$ | B. | ±1 | C. | $±\sqrt{3}$ | D. | $±\frac{{\sqrt{3}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
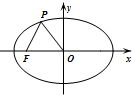 如图,已知椭圆C的中心为原点O,F(-2$\sqrt{5}$,0)为C的左焦点,P为C上一点,满足|OP|=|OF|且|PF|=4,则椭圆C的方程为( )
如图,已知椭圆C的中心为原点O,F(-2$\sqrt{5}$,0)为C的左焦点,P为C上一点,满足|OP|=|OF|且|PF|=4,则椭圆C的方程为( )| A. | $\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{5}$=1 | B. | $\frac{{x}^{2}}{30}$+$\frac{{y}^{2}}{10}$=1 | C. | $\frac{{x}^{2}}{36}$+$\frac{{y}^{2}}{16}$=1 | D. | $\frac{{x}^{2}}{45}$+$\frac{{y}^{2}}{25}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 单调递减且无最小值 | B. | 单调递减且有最小值 | ||
| C. | 单调递增且无最大值 | D. | 单调递增且有最大值 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com