[题目]某地区山体大面积滑坡.政府准备调运一批赈灾物资共装26辆车.从某市出发以v的速度匀速直达灾区.如果两地公路长400km.且为了防止山体再次坍塌.每两辆车的间距保持在( )2km．设物资全部运抵灾区的时间为y小时.请建立y关于每车平均时速v的函数关系式.并求出车辆速度为多少千米/小时.物资能最快送到灾区? 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】某地区山体大面积滑坡，政府准备调运一批赈灾物资共装26辆车，从某市出发以v（km/h）的速度匀速直达灾区，如果两地公路长400km，且为了防止山体再次坍塌，每两辆车的间距保持在（）2km．（车长忽略不计）设物资全部运抵灾区的时间为y小时，请建立y关于每车平均时速v（km/h）的函数关系式，并求出车辆速度为多少千米/小时，物资能最快送到灾区？

【答案】解：设全部物资到达灾区所需时间为t小时，由题意可知，y相当于：最后一辆车行驶了25个（）2km+400km所用的时间，
因此y= = + ，
因为y= + ≥2 =10，
当且仅当，即v=80时取“=”．
故这些汽车以80km/h的速度匀速行驶时，物资能最快送到灾区
【解析】由题意可知，y相当于：最后一辆车行驶了25个（）2km+400km所用的时间，即可得到函数的解析式，利用基本不等式，即可得出结论．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】小明同学在寒假社会实践活动中，对白天平均气温与某家奶茶店的品牌饮料销量之间的关系进行了分析研究，他分别记录了1月11日至1月15日的白天气温（）与该奶茶店的品牌饮料销量（杯），得到如表数据：

日期	1月11号	1月12号	1月13号	1月14号	1月15号
平均气温（）	9	10	12	11	8
销量（杯）	23	25	30	26	21

（1）若先从这五组数据中抽出2组，求抽出的2组数据恰好是相邻2天数据的概率；

（2）请根据所给五组数据，求出关于的线性回归方程式；

（3）根据（2）所得的线性回归方程，若天气预报1月16号的白天平均气温为，请预测该奶茶店这种饮料的销量.

（参考公式：，）

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图是利用斜二测画法画出的△ABO的直观图，已知O′B′=4，且△ABO的面积为16，过A′作A′C′⊥x′轴，则A′C′的长为（）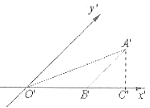

A.
B.
C.
D.1

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】在直角坐标系中，已知中心在原点，离心率为的椭圆的一个焦点为圆：的圆心．

（Ⅰ）求椭圆的方程；

（Ⅱ）设是椭圆上一点，过作两条斜率之积为的直线，，当直线，都与圆相切时，求的坐标．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图，在平面直角坐标系xoy中，已知F1 ， F2分别是椭圆E：的左、右焦点，A，B分别是椭圆E的左、右顶点，且．

（1）求椭圆E的离心率；
（2）已知点D（1，0）为线段OF2的中点，M 为椭圆E上的动点（异于点A、B），连接MF1并延长交椭圆E于点N，连接MD、ND并分别延长交椭圆E于点P、Q，连接PQ，设直线MN、PQ的斜率存在且分别为k1、k2 ，试问是否存在常数λ，使得k1+λk2=0恒成立？若存在，求出λ的值；若不存在，说明理由．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】为了估计某校的一次数学考试情况，现从该校参加考试的600名学生中随机抽出60名学生，其成绩（百分制）均在[40，100）上，将这些成绩分成六段[40，50），[50，60）…[90，100），后得到如图所示部分频率分布直方图．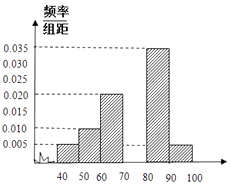

（1）求抽出的60名学生中分数在[70，80）内的人数；
（2）若规定成绩不小于85分为优秀，则根据频率分布直方图，估计该校优秀人数．
（3）根据频率分布直方图算出样本数据的中位数．