练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在三棱柱中， ， ， 为的中点.

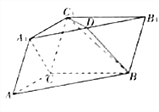
    （1）证明： 平面；

    （2）若，点在平面的射影在上，且侧面的面积为，求三棱锥的体积.

    【答案】（1）见解析;（2）.

    【解析】试题分析：（1）连接交于点，连接.利用中点可得，所以平面.（2）取中点，连接，过点作于，连接,利用等腰三角形和射影的概念可知平面，所以，所以平面，所以.利用侧面的面积可计算得三棱锥的高，由此可计算得三棱锥的体积.

    试题解析：

    （1）证明：连接交于点，连接.

    则为的中点，又为的中点，所以，且平面， 平面，则平面.

    （2）解：取的中点，连接，过点作于点，连接.

    因为点在平面的射影在上，且，

    所以平面，∴， ，∴平面，

    则.

    设，在中， ， ，

    ∴， ， ，

    由，可得.

    则

    .

    所以三棱锥的体积为.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知数列{an}是首项为a1= ，公比q= 的等比数列，设bn+2=3log an（n∈N*），数列{cn}满足cn=anbn ．
    （1）求证：{bn}是等差数列；
    （2）求数列{cn}的前n项和Sn；
    （3）若cn≤ +m﹣1对一切正整数n恒成立，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=3x2﹣2ax﹣b，其中a，b是实数．
    （1）若不等式f（x）≤0的解集是[0，6]，求ab的值；
    （2）若b=3a，对任意x∈R，都有f（x）≥0，且存在实数x，使得f（x）≤2﹣ a，求实数a的取值范围；
    （3）若方程有一个根是1，且a，b＞0，求 的最小值，及此时a，b的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某地区山体大面积滑坡，政府准备调运一批赈灾物资共装26辆车，从某市出发以v（km/h）的速度匀速直达灾区，如果两地公路长400km，且为了防止山体再次坍塌，每两辆车的间距保持在（ ）2km．（车长忽略不计）设物资全部运抵灾区的时间为y小时，请建立y关于每车平均时速v（km/h）的函数关系式，并求出车辆速度为多少千米/小时，物资能最快送到灾区？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】山西某公司有一批专业技术人员，对他们进行年龄状况和接受教育程度（本科学历）的调查，其结果（人数分布）如表：

    学历

    35岁以下

    3550岁

    50岁以上

    本科

    80

    30

    20

    研究生

    20

    （Ⅰ）用分层抽样的方法在岁年龄段的专业技术人员中抽取一个容量为10的样本，将该样本看成一个总体，从中任取3人，求至少有1人的学历为研究生的概率；

    （Ⅱ）在这个公司的专业技术人员中按年龄状况用分层抽样的方法抽取个人，其中35岁以下48人，50岁以上10人，再从这个人中随机抽取出1人，此人的年龄为50岁以上的概率为，求、的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某化工厂生产的某种化工产品，当年产量在150吨至250吨之间，其生产的总成本y（万元）与年产量x（吨）之间的函数关系式可近似地表示为
    问：
    （1）年产量为多少吨时，每吨的平均成本最低？并求出最低成本？
    （2）若每吨平均出厂价为16万元，则年产量为多少吨时，可获得最大利润？并求出最大利润？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设直线x=t与函数f（x）=x2 ， g（x）=lnx的图象分别交于点M，N，则当|MN|达到最小时t的值为 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】根据下列条件，分别写出椭圆的标准方程：
    （1）与椭圆 有公共焦点，且过M（3，﹣2）；
    （2）中心在原点，焦点在坐标轴上，且经过两点 和 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】【2017广西5月考前联考】宝宝的健康成长是妈妈们最关心的问题，父母亲为婴儿选择什么品牌的奶粉一直以来都是育婴中的一个重要话题，为了解过程奶粉的知名度和消费者的信任度，某调查小组特别调查记录了某大型连锁超市2015年与2016年这两年销售量前5名的五个品牌奶粉的销量（单位：罐），绘制如下的管状图：

    （1）根据给出的这两年销量的管状图，对该超市这两年品牌奶粉销量的前五强进行排名；

    （2）分别计算这5个品牌奶粉2016年所占总销量（仅指这5个品牌奶粉的总销量）的百分比（百分数精确到各位），并将数据填入如下饼状图中的括号内；

    （3）试以（2）中的百分比作为概率，若随机选取2名购买这5个品牌中任意1个品牌的消费者进行采访，记为被采访中购买飞鹤奶粉的人数，求的分布列及数学期望.

    查看答案和解析>>

    同步练习册答案