
(08年黄冈中学一模文) (12分) 如图,在梯形ABCD中,AB∥CD,AD=DC=CB=a , ∠ABC=60°.平面ACEF⊥平面ABCD,且四边形ACEF是矩形,AF=a.
(I)求证:AC⊥BE;
(II)求二面角B-EF-D的余弦值.

解析:(I)∵AB∥CD,AD=DC=CB=a,∴四边形ABCD是等腰梯形.设AC交BD于N,连EN.
∵∠ABC=60°,∴∠DCB=∠ADC=120°,∠DAC=∠ACD=30°,
∴AC=![]() ,AB=2a,
,AB=2a,![]() =90°.
=90°.
又四边形ACEF是矩形,
∴AC⊥平面BCE.∴AC⊥BE.
(II)∵平面ACEF⊥平面ABCD, EC⊥AC,
∴EC⊥面 ABCD,∴EC⊥CD, EC⊥AD,又AF∥CE,
∴AF⊥AD,而AF=CE,AD=CD,
∴Rt△![]() ≌Rt△
≌Rt△![]() ,DE=DF.
,DE=DF.
过D作DG⊥EF于G,则G为EF的中点,于是EG=![]() .
.
在Rt△![]() 中,
中,![]()
![]() ,∴
,∴![]() .∴
.∴![]() .
.
设所求二面角大小为![]() ,则由
,则由![]() 及
及![]() ,
,![]() 得,
得,![]() ,
,
www.ks5u.com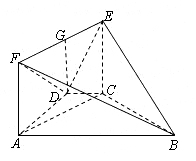


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
(08年黄冈中学一模理) (本小题满分12分)一个袋子中装有m个红球和n个白球(m>n≥4),它们除颜色不同外,其余都相同,现从中任取两个球.
(1)若取出两个红球的概率等于取出一红一白两个球的概率的整数倍,求证:m必为奇数;
(2)若取出两个球颜色相同的概率等于取出两个颜色不同的概率,求满足m+n≤20的所有数组(m, n)查看答案和解析>>
科目:高中数学 来源: 题型:
(08年黄冈中学一模理) (本小题满分14分)对于函数f(x),若存在![]() ,使
,使![]() 成立,则称x0为f(x)的不动点. 如果函数
成立,则称x0为f(x)的不动点. 如果函数![]() 有且仅有两个不动点0,2,且
有且仅有两个不动点0,2,且![]()
(1)试求函数f(x)的单调区间;
(2)已知各项不为零且不为1的数列{an}满足![]() ,求证:
,求证:![]() ;
;
(3)设![]() ,
,![]() 为数列{bn}的前n项和,求证:
为数列{bn}的前n项和,求证:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年黄冈中学一模文) (14分)已知椭圆![]() 过定点A(1,0),焦点在x轴上,且离心率e满足
过定点A(1,0),焦点在x轴上,且离心率e满足![]() .
.
(I)求![]() 的取值范围;
的取值范围;
(II)若椭圆与![]() 的交于点B,求点B的横坐标的取值范围;
的交于点B,求点B的横坐标的取值范围;
(Ⅲ)在条件(II)下,现有以A为焦点,过点B且开口向左的抛物线,抛物线的顶点坐标为M(m,0),求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com