
{an},{bn}都是各项为正数的数列,对任意的自然数n,都有an、bn2、an+1成等差数列,bn2、an+1、bn+12成等比数列.
(1)试问{bn}是否是等差数列?为什么?
(2)求证:对任意的自然数p,q(p>q),bp-q2+bp+q2≥2bp2成立;
(3)如果a1=1,b1=![]() ,
,![]() ,求
,求![]() .
.
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:高中数学 来源: 题型:
(12分)设数列{an},{bn}都是等差数列,它们的前n项的和分别为Sn , Tn ,若对一切n ∈ N*,都有Sn+3 = Tn .(1)若a1 ≠ b1,试分别写出一个符号条件的数列{an}和{bn};(2)若a1 + b1 = 1,数列{cn}满足:cn = 4 an + l(–1)n–12 bn,且当n ∈ N*时,cn+1 ≥ cn恒成立,求实数l的最大值.
查看答案和解析>>
科目:高中数学 来源:2010-2011年广西省桂林中学高二下学期期中考试数学 题型:解答题
(本小题满分12分)
已知点Pn(an,bn)都在直线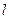 :y=2x+2上,P1为直线
:y=2x+2上,P1为直线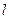 与x轴的交点,数列
与x轴的交点,数列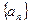 成等差数列,公差为1.(n∈N+)
成等差数列,公差为1.(n∈N+)
(1)求数列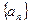 ,
,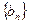 的通项公式;
的通项公式;
(2)若f(n)= 问是否存在k
问是否存在k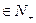 ,使得f(k+5)=2f(k)-2成立;若存在,求出
,使得f(k+5)=2f(k)-2成立;若存在,求出 k的值,若不存在,说明理由。
k的值,若不存在,说明理由。
(3)求证: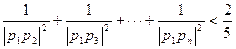 (n≥2,n∈N+)
(n≥2,n∈N+)
查看答案和解析>>
科目:高中数学 来源:2012年全国普通高等学校招生统一考试理科数学(江西卷解析版) 题型:填空题
设数列{an},{bn}都是等差数列,若a1+b1=7,a3+b3=21,则a5+b5=_________
查看答案和解析>>
科目:高中数学 来源:2010-2011年广西省高二下学期期中考试数学 题型:解答题
(本小题满分12分)
已知点Pn(an,bn)都在直线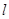 :y=2x+2上,P1为直线
:y=2x+2上,P1为直线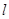 与x轴的交点,数列
与x轴的交点,数列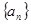 成等差数列,公差为1.(n∈N+)
成等差数列,公差为1.(n∈N+)
(1)求数列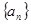 ,
,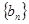 的通项公式;
的通项公式;
(2)若f(n)=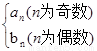 问是否存在k
问是否存在k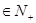 ,使得f(k+5)=2f(k)-2成立;若存在,求出k的值,若不存在,说明理由。
,使得f(k+5)=2f(k)-2成立;若存在,求出k的值,若不存在,说明理由。
(3)求证: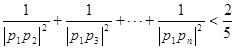 (n≥2,n∈N+)
(n≥2,n∈N+)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com