
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数)以坐标原点
为参数)以坐标原点![]() 为极点,
为极点, ![]() 轴正半轴为极轴建立极坐标系.
轴正半轴为极轴建立极坐标系.
(1)求曲线![]() 的普通方程和极坐标方程;
的普通方程和极坐标方程;
(2)直线![]() 的极坐标方程为
的极坐标方程为![]() ,若
,若![]() 与
与![]() 的公共点为
的公共点为![]() ,且
,且![]() 是曲线
是曲线![]() 的中心,求
的中心,求![]() 的面积.
的面积.
【答案】(1)![]() ,
, ![]() .(2)
.(2)![]() .
.
【解析】试题分析:曲线![]() 的参数方程利用平方法消去参数
的参数方程利用平方法消去参数![]() ,得其普通方程,将
,得其普通方程,将![]() ,
, ![]() 代入普通方程并化简,可得其极坐标方程;(2)将
代入普通方程并化简,可得其极坐标方程;(2)将![]() 代入极坐标方程可得
代入极坐标方程可得![]() ,根据极径的几何意义利用韦达定理可得
,根据极径的几何意义利用韦达定理可得![]() ,再根据点到直线距离公式及三角形面积公式可得结果.
,再根据点到直线距离公式及三角形面积公式可得结果.
试题解析:(1)由曲线![]() 的参数方程消去参数
的参数方程消去参数![]() ,得其普通方程为
,得其普通方程为![]() .
.
将![]() ,
, ![]() 代入上式并化简,得其极坐标方程为
代入上式并化简,得其极坐标方程为![]() .
.
(2)将![]() 代入得
代入得![]() .
.
得![]() .
.
设![]() ,
, ![]() ,则
,则![]() ,
, ![]() ,
,
所以![]() .
.
又由(1),知![]() ,且由(2)知直线
,且由(2)知直线![]() 的直角坐标方程为
的直角坐标方程为![]() ,所以
,所以![]() 到
到![]() 的距离是
的距离是 ,所以
,所以![]() 的面积
的面积![]() .
.
【名师点晴】参数方程主要通过代入法或者已知恒等式(如![]() 等三角恒等式)消去参数化为普通方程,通过选取相应的参数可以把普通方程化为参数方程,利用关系式
等三角恒等式)消去参数化为普通方程,通过选取相应的参数可以把普通方程化为参数方程,利用关系式![]() ,
,  等可以把极坐标方程与直角坐标方程互化,本题这类问题一般我们可以先把曲线方程化为直角坐标方程,用直角坐标方程解决相应问题.
等可以把极坐标方程与直角坐标方程互化,本题这类问题一般我们可以先把曲线方程化为直角坐标方程,用直角坐标方程解决相应问题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】“水是生命之源”,但是据科学界统计可用淡水资源仅占地球储水总量的![]() ,全世界近
,全世界近![]() 人口受到水荒的威胁.某市为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准
人口受到水荒的威胁.某市为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准![]() (吨):一位居民的月用水量不超过
(吨):一位居民的月用水量不超过![]() 的部分按平价收费,超出
的部分按平价收费,超出![]() 的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照
的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照![]() 分成9组,制成了如图所示的频率分布直方图.
分成9组,制成了如图所示的频率分布直方图.

(1)求直方图中![]() 的值;
的值;
(2)设该市有60万居民,估计全市居民中月均用水量不低于2.5吨的人数,并说明理由;
(3)若该市政府希望使![]() 的居民每月的用水不按议价收费,估计
的居民每月的用水不按议价收费,估计![]() 的值,并说明理由.
的值,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() (
(![]() )的离心率是
)的离心率是![]() ,点
,点![]() 在短轴
在短轴![]() 上,且
上,且![]() 。
。
(1)球椭圆![]() 的方程;
的方程;
(2)设![]() 为坐标原点,过点
为坐标原点,过点![]() 的动直线与椭圆交于
的动直线与椭圆交于![]() 两点。是否存在常数
两点。是否存在常数![]() ,使得
,使得![]() 为定值?若存在,求
为定值?若存在,求![]() 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个命题:
①函数y=2sin![]() 的图象的一条对称轴是x=
的图象的一条对称轴是x=![]() ;
;
②函数y=tanx的图象关于点![]() 对称;
对称;
③若sin![]() =sin
=sin![]() ,则x1-x2=kπ,其中k∈Z;
,则x1-x2=kπ,其中k∈Z;
④函数![]() ,x∈[0,2π]的图象与直线y=k有且仅有两个不同的交点,则k的取值范围为(1,3).
,x∈[0,2π]的图象与直线y=k有且仅有两个不同的交点,则k的取值范围为(1,3).
其中正确的有____(填写所有正确命题的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】正方体ABCD - A1B1C1D1的棱长为2, E、F、G分别为BC、CC1、BB1的中点,则( )
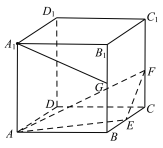
A.直线![]() 与直线AF垂直B.直线A1G与平面AEF平行
与直线AF垂直B.直线A1G与平面AEF平行
C.平面![]() 截正方体所得的截面面积为
截正方体所得的截面面积为![]() D.点C与点G到平面AEF的距离相等
D.点C与点G到平面AEF的距离相等
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com