练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    4．在平面直角坐标系xOy中，圆C的参数方程为$\left\{\begin{array}{l}x=2sint\\ y=2cost\end{array}\right.，（t为参数）$，在以原点O为极点，x轴的非负半轴为极轴建立的极坐标系中，直线l的极坐标方程为$ρsin（θ+\frac{π}{4}）=2\sqrt{2}$，A（2，0）
    （Ⅰ）求圆C的普通方程和直线l的直角坐标方程；
    （Ⅱ） AP是圆C上动弦，求AP中点M到l距离的最小值．

    分析 （Ⅰ）利用三种方程的转化方法，求圆C的普通方程和直线l的直角坐标方程；
    （Ⅱ） 设P（2cosα，2sinα），则M（cosα+1，sinα），利用点到直线的距离公式，即可求线段AP的中点M到直线l的距离的最小值．

    解答 解：（Ⅰ）消去参数得，圆C的普通方程得x2+y2=4． 直线l的极坐标方程为$ρsin（θ+\frac{π}{4}）=2\sqrt{2}$，直角坐标方程为x+y-4=0；
    （Ⅱ）设P（2cosα，2sinα），则M（cosα+1，sinα），
    ∴d=$\frac{|cosα+sinα-3|}{\sqrt{2}}$=$\frac{|\sqrt{2}sin（α+45°）-3|}{\sqrt{2}}$，
    ∴最小值是$\frac{3-\sqrt{2}}{\sqrt{2}}$=$\frac{3\sqrt{2}-2}{2}$．…（10分）

    点评 本题考查参数方程、普通方程、极坐标方程的转化，考查点到直线的距离公式，考查学生的计算能力，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

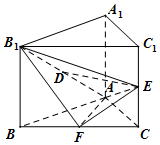    10．已知直三棱柱ABC-A1B1C1中，△ABC为等腰直角三角形，∠BAC=90°，且AB=AA1，D、E、F分别为B1A、C1C、BC的中点．
    （1）求证：直线DE∥平面ABC；
    （2）求锐二面角B1-AE-F的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．已知g（x）=（x-e）2（e＞0），f（x）=lnx+bx．
    （1）讨论f（x）的单调性；
    （2）当b=0时，记k（x）=$\frac{g（x）}{f（x）}$，已知k（x）有三个极值点，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．在6件产品中有2件次品，连续抽3次，每次抽1件，求：
    （1）不放回抽样时，抽到次品数ξ的分布列；
    （2）放回抽样时，抽到次品数η的分布列．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．在等比数列{an}中，a1=1，且a2是a1与a3-1的等差中项．
    （1）求数列{an}的通项公式；
    （2）若数列{bn}满足bn=$\frac{n（n+1）{a}_{n}+1}{n（n+1）}$，（n∈N*）．求数列{bn}的前n项和Sn．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．直线3x+4y-2=0和直线6x+8y+1=0的距离是（　　）
    A．$\frac{3}{5}$B．$\frac{1}{2}$C．$\frac{3}{10}$D．$\frac{1}{5}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．如图，在直三棱柱ABC-A1B1C1中，AB=BC=2$\sqrt{2}，C{C_1}$=4，∠ABC=90°，E，F分别为AA1，C1B1的中点，沿棱柱的表面从点E到点F的最短路径的长度为（　　）
    A．$\sqrt{14+4\sqrt{2}}$B．$\sqrt{22}$C．$3\sqrt{2}$D．$2\sqrt{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．已知$f（x）=3sin（{ωx+\frac{π}{6}}）（{ω＞0}）$，若f（x）图象向左平移$\frac{π}{6}$个单位后图象与y=3cosωx图象重合．
    （1）求ω的最小值；
    （2）在条件（1）下将下表数据补充完整，并用“五点法”作出f（x）在一个周期内的图象．
    $ωx+\frac{π}{6}$0$\frac{π}{2}$π$\frac{3π}{2}$2π
    x
    f（x）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．在某商业促销的最后一场活动中，甲、乙、丙、丁、戊、己6名成员随机抽取4个礼品，每人最多抽一个礼品，且礼品中有两个完全相同的笔记本电脑，两个完全相同的山地车，则甲、乙两人都抽到礼品的情况有（　　）
    A．36种B．24种C．18种D．9种

    查看答案和解析>>

    同步练习册答案