
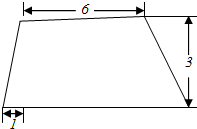
 已知一圆台的轴截面如图所示,则它的内接四棱台体积的最大值为( )
已知一圆台的轴截面如图所示,则它的内接四棱台体积的最大值为( )| A. | 37 | B. | 74 | C. | 111 | D. | 222 |
分析 由题意,内接四棱台体积的最大时,上下底面为圆的内接正方形,其边长分别为3$\sqrt{2}$,4$\sqrt{2}$,求出截去圆锥的高,即可求出内接四棱台体积的最大值.
解答 解:由题意,内接四棱台体积的最大时,上下底面为圆的内接正方形,其边长分别为3$\sqrt{2}$,4$\sqrt{2}$,
设截去圆锥的高为h,根据相似形,可得截去圆锥的高为$\frac{h}{h+3}=\frac{6}{8}$,∴h=9,
∴内接四棱台体积的最大值为$\frac{1}{3}•(4\sqrt{2})^{2}•12-\frac{1}{3}•(3\sqrt{2})^{2}•9$=74,
故选:B.
点评 本题考查内接四棱台体积的最大值,考查学生的计算能力,确定内接四棱台体积的最大时,上下底面为圆的内接正方形,其边长分别为3$\sqrt{2}$,4$\sqrt{2}$,求出截去圆锥的高是关键.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(α+$\frac{5π}{6}$)>f(α+$\frac{π}{12}$) | B. | f(α+$\frac{5π}{6}$)<f(α+$\frac{π}{12}$) | C. | f(α+$\frac{5π}{6}$)=f(α+$\frac{π}{12}$) | D. | 大小与α,φ有关 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 地区 | A | B | C |
| 数量 | 50 | 150 | 100 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com