
分析 法一、先根据几何概型的概率公式求出在区间[0,2]中随机地取一个数,这个数大于$\frac{1}{2}$的概率,进一步求出两个数都大于$\frac{1}{2}$的概率,则这两个数中较小的数小于$\frac{1}{2}$的概率可求;
法二、设所取两数分别为x,y,则$\left\{\begin{array}{l}{0≤x≤2}\\{0≤y≤2}\end{array}\right.$,排除$\left\{\begin{array}{l}{x≥\frac{1}{2}}\\{y≥\frac{1}{2}}\end{array}\right.$,画出图形,数形结合可得两个数中较小的数小于$\frac{1}{2}$的概率.
解答 解:法一、∵在区间[0,2]中随机地取一个数,这个数大于$\frac{1}{2}$的概率为$\frac{\frac{3}{2}}{2}=\frac{3}{4}$,
∴在区间[0,2]中随机地取两个数,则这两个数都大于$\frac{1}{2}$的概率为$\frac{3}{4}×\frac{3}{4}=\frac{9}{16}$,
∴这两个数中较小的数小于$\frac{1}{2}$的概率是1-$\frac{9}{16}$=$\frac{7}{16}$;
法二、
设所取两数分别为x,y,则$\left\{\begin{array}{l}{0≤x≤2}\\{0≤y≤2}\end{array}\right.$,
若两数中较小的数小于$\frac{1}{2}$,则还需满足x$<\frac{1}{2}$或y$<\frac{1}{2}$,只需排除$\left\{\begin{array}{l}{x≥\frac{1}{2}}\\{y≥\frac{1}{2}}\end{array}\right.$,
作出可行域如图: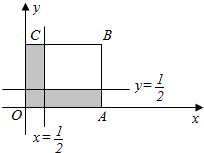
∴这两个数中较小的数小于$\frac{1}{2}$的概率是1-$\frac{\frac{3}{2}×\frac{3}{2}}{4}$=$\frac{7}{16}$.
故答案为:$\frac{7}{16}$.
点评 本题主要考查了几何概型,简单地说,如果每个事件发生的概率只与构成该事件区域的长度(面积或体积)成比例,则称这样的概率模型为几何概率模型,简称为几何概型.该题属于中档题.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | $\frac{5}{9}$ | C. | $\frac{29}{9}$ | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{20}{7}$ | B. | $\frac{12}{7}$ | C. | $\frac{16+4\sqrt{2}}{7}$ | D. | $\frac{16-4\sqrt{2}}{7}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com