
(本题满分15分)等比数列{![]() }的前n项和为
}的前n项和为![]() , 已知对任意的
, 已知对任意的![]() ,点
,点![]() ,均在函数
,均在函数![]() 且
且![]() 均为常数)的图像上.
均为常数)的图像上.
(1)求r的值;
(11)当b=2时,记 ![]() 证明:
证明:
对任意的![]() ,不等式
,不等式![]() 成立
成立
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2012届浙江省桐乡市高级中学高三10月月考理科数学 题型:解答题
(本题满分15分)已知各项均不相等的等差数列 的前四项和
的前四项和 ,且
,且 成等比.
成等比.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)设 为数列
为数列 的前n项和,若
的前n项和,若 对一切
对一切 恒成立,求实数
恒成立,求实数 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年浙江省分校高三10月学习质量诊断理科数学试卷(解析版) 题型:解答题
(本题满分15分)
在等比数列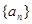 中,
中,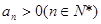 ,公比
,公比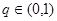 ,且
,且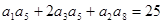 ,
,
又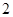 是
是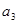 与
与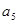 的等比中项。设
的等比中项。设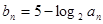 .
.
(Ⅰ) 求数列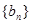 的通项公式;
的通项公式;
(Ⅱ) 已知数列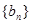 的前
的前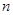 项和为
项和为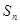 ,
,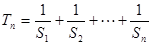 ,求
,求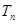 .
.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年浙江省桐乡市高三10月月考理科数学 题型:解答题
(本题满分15分)已知各项均不相等的等差数列 的前四项和
的前四项和 ,且
,且 成等比.
成等比.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)设 为数列
为数列 的前n项和,若
的前n项和,若 对一切
对一切 恒成立,求实数
恒成立,求实数 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年浙江省六校高三第一次联考文科数学 题型:解答题
(本题满分15分)
设抛物线M方程为 ,其焦点为F,P(
,其焦点为F,P(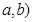 (
( 为直线
为直线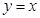 与抛物线M的一个交点,
与抛物线M的一个交点,
(1)求抛物线的方程;
(2)过焦点F的直线 与抛物线交于A,B两点,试问在抛物线M的准线上是否存在一点Q,使得
与抛物线交于A,B两点,试问在抛物线M的准线上是否存在一点Q,使得 QAB为等边三角形,若存在求出Q点的坐标,若不存在请说明理由.
QAB为等边三角形,若存在求出Q点的坐标,若不存在请说明理由.
查看答案和解析>>
科目:高中数学 来源:2012届江苏省高三第一学期第一次学情调研理科数学试卷 题型:解答题
(本题满分15分)某经销商用一辆J型卡车将某种水果从果园运送(满载)到相距400km的水果批发市场.据测算,J型卡车满载行驶时,每100km所消耗的燃油量u(单位:
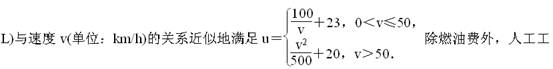
资、车损等其他费用平均每小时300元.已知燃油价格为每升(L)7.5元.
(1)设运送这车水果的费用为y(元)(不计返程费用),将y表示成速度v的函数关系式;
(2)卡车该以怎样的速度行驶,才能使运送这车水果的费用最少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com