
分析 (1)把参数方程化为普通方程,把极坐标方程化为直角坐标方程,由曲线C1与C2只有一个公共点,可得方程组有唯一解,判别式等于零,从而求得t的值.
(2)在曲线C1上任意取一点A(m,m2-1),则A到C2 :x+y=t的距离为d=$\frac{|m{+m}^{2}-1+2|}{\sqrt{2}}$=$\frac{{|(m+\frac{1}{2})}^{2}+\frac{3}{4}|}{\sqrt{2}}$,再利用二次函数的性质求得A到C2 的距离d取得最小值.
解答 解:(1)曲线C1的参数方程为$\left\{\begin{array}{l}{x=sinφ+cosφ}\\{y=sin2φ}\end{array}\right.$ (φ 为参数),即x2=1+y,即 y=x2-1.
由曲线C2的极坐标方程为:ρsin(θ+$\frac{π}{4}$)=$\frac{\sqrt{2}}{2}$t(其中t为常数),可得$\frac{\sqrt{2}}{2}$ρsinθ+$\frac{\sqrt{2}}{2}$ρcosθ=$\frac{\sqrt{2}}{2}$t,
即 x+y=t.
根据曲线C1与C2只有一个公共点,可得 $\left\{\begin{array}{l}{x+y=t}\\{y{=x}^{2}-1}\end{array}\right.$ 有唯一解,即x2+x-t-1=0有唯一解,
∴△=1+4(t+1)=0,求得t=-$\frac{5}{4}$.
(2)当t=-2时,曲线C2 即:x+y=-2,在曲线C1:y=x2-1 上任意取一点A(m,m2-1),
则A到C2 :x+y=t的距离为d=$\frac{|m{+m}^{2}-1+2|}{\sqrt{2}}$=$\frac{{|(m+\frac{1}{2})}^{2}+\frac{3}{4}|}{\sqrt{2}}$,故当m=-$\frac{1}{2}$时,A到C2 :x+y=t的距离d取得最小值为$\frac{3\sqrt{2}}{8}$.
点评 本题主要考查把参数方程化为普通方程的方法,把极坐标方程化为直角坐标方程的方法,二次函数的性质应用,属于基础题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{2}{3}$,1) | B. | [$\frac{1}{3}$,$\frac{\sqrt{2}}{2}$] | C. | [$\frac{1}{3}$,1) | D. | (0,$\frac{1}{3}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
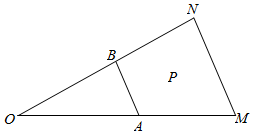 如图,在△OMN中,A,B分别是OM,ON中点,若$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$(x,y∈R),且点P落在四边形ABNM内(含边界),则x2+y2的取值范围是( )
如图,在△OMN中,A,B分别是OM,ON中点,若$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$(x,y∈R),且点P落在四边形ABNM内(含边界),则x2+y2的取值范围是( )| A. | [1,2] | B. | [1,4] | C. | $[\frac{1}{2},1]$ | D. | $[\frac{1}{2},4]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
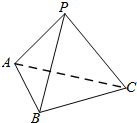 如图在三棱锥P-ABC中,PA⊥PB,PA⊥PC,PC⊥PB,PA=1,PB=2,PC=2,则该棱锥外接球的体积为$\frac{9}{2}π$.
如图在三棱锥P-ABC中,PA⊥PB,PA⊥PC,PC⊥PB,PA=1,PB=2,PC=2,则该棱锥外接球的体积为$\frac{9}{2}π$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com