
设函数
(1)解不等式 ;
;
(2)求函数 的最小值.
的最小值.
(1) ;(2)
;(2)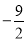 .
.
【解析】
试题分析:(1)解含绝对值的不等式,关键是去掉绝对值符号,其方法有三种:①定义法;②平方法;③分区间讨论法,这里用的是分区间讨论法,遇到多个绝对值时常用此方法;(2)求绝对值函数的值域,通常是通过分区间讨论,去掉绝对值符号,将绝对值函数改写成分段函数,然后就每段求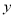 的范围,最后再将每段求得的范围求并集,注意不是求交集,从而得到绝对值函数的值域.
的范围,最后再将每段求得的范围求并集,注意不是求交集,从而得到绝对值函数的值域.
试题解析:(1)不等式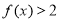 等价于:
等价于:
①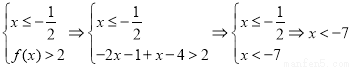 ;
;
②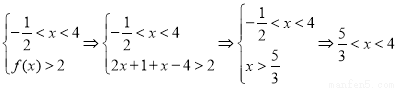 ;
;
③ ,
,
综合①②③得不等式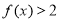 的解集为:
的解集为:
(2)①当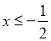 时,
时, ;
;
②当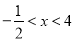 时,
时,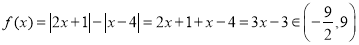
③当 时,
时,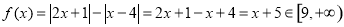
综合①②③得函数 的值域为
的值域为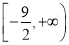 ,因此求函数
,因此求函数 的最小值为
的最小值为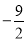 .
.
考点:1.含绝对值的不等式的解法;2.绝对值函数的值域的求法;3.分类讨论思想.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源:2015届吉林省长春市新高三起点调研考试理科数学试卷(解析版) 题型:选择题
已知数列 为等差数列,其前
为等差数列,其前 项和为
项和为 ,若
,若 ,
, ,则该等差数列的公差
,则该等差数列的公差 ( )
( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2015届吉林省长春市新高三起点调研考试文科数学试卷(解析版) 题型:选择题
过抛物线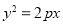
 的焦点
的焦点 作直线与此抛物线相交于
作直线与此抛物线相交于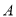 、
、 两点,
两点, 是坐标原点,当
是坐标原点,当 时,直线
时,直线 的斜率的取值范围是( )
的斜率的取值范围是( )
A. B.
B.
C.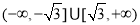 D.
D.
查看答案和解析>>
科目:高中数学 来源:2015届吉林省长春市高二下学期期末考试理科数学试卷(解析版) 题型:解答题
甲、乙两人参加某电视台举办的答题闯关游戏,按照规则,甲先从6道备选题中一次任意抽取3道题,独立作答,然后由乙回答剩余3题,每人答对其中的2题就停止答题,即闯关成功。已知6道备选题中,甲能答对其中的4道题,乙答对每道题的概率都是 .
.
(1)求甲、乙至少有一人闯关成功的概率;
(2)设甲答对题目的个数为 ,求
,求 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源:2015届吉林省长春市高二下学期期末考试理科数学试卷(解析版) 题型:选择题
已知函数 的两个极值点分别为
的两个极值点分别为 ,且
,且 ,点
,点 表示的平面区域为
表示的平面区域为 ,若函数
,若函数 (
( )的图象上存在区域
)的图象上存在区域 内的点,则实数
内的点,则实数 的取值范围是( )
的取值范围是( )
A. B.
B. C.
C. D.
D.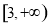
查看答案和解析>>
科目:高中数学 来源:2015届吉林省长春市高二下学期期末考试文科数学试卷(解析版) 题型:解答题
某校高三年级有男学生105人,女学生126人,教师42人,用分层抽样的方法从中抽取13人进行问卷调查,设其中某项问题的选择,分别为“同意”、“不同意”两种,且每人都做了一种选择,下面表格中提供了被调查人答卷情况的部分信息.
| 同意 | 不同意 | 合计 |
教师 | 1 |
|
|
女学生 |
| 4 |
|
男学生 |
| 2 |
|
(1)完成此统计表;(2分)
(2)估计高三年级学生“同意”的人数;(4分)
(3)从被调查的女学生中选取2人进行访谈,求选到两名学生中恰有一人“同意”,一人“不同意”的概率.(6分)
查看答案和解析>>
科目:高中数学 来源:2015届吉林省长春市高二下学期期中考试文科数学试卷(解析版) 题型:解答题
已知椭圆 的离心率
的离心率 ,
, 分别为椭圆的长轴和短轴的端点,
分别为椭圆的长轴和短轴的端点, 为
为 中点,
中点, 为坐标原点,且
为坐标原点,且 .
.
(1)求椭圆的方程;
(2)过点 的直线
的直线 交椭圆于
交椭圆于 两点,求
两点,求 面积最大时,直线
面积最大时,直线 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com