
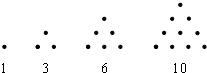
 传说古希腊毕达哥拉斯学派的数学家经常在沙滩上面画点或用小石子表示数.他们研究过如图的三角形数:
传说古希腊毕达哥拉斯学派的数学家经常在沙滩上面画点或用小石子表示数.他们研究过如图的三角形数:分析 先归纳出数列an=$\frac{n(n+1)}{2}$,然后写出:
b1=a4,b2=a5,
b3=a9,b4=a10,
b5=a14,b6=a15,
…
再归纳出b2n=a5n,b2n-1=a5n-1.
解答 解:显然an=$\frac{n(n+1)}{2}$,数列an中是5的倍数要么n+1是5的倍数,要么n是5的倍数,
b1=a4,b2=a5,
b3=a9,b4=a10,
b5=a14,b6=a15,
…
∴b2n=a5n,b2n-1=a5n-1,
∴b2014是数列{an}中的第2014÷2×5=5035项.
∴b2n-1=$\frac{5n(5n-1)}{2}$.
点评 本题主要考查归纳推理的思维能力.


 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:高中数学 来源: 题型:选择题
| A. | 对于命题p:?x∈R,x2+x+1>0 则¬p:?x∈R,x2+x+1≤0 | |
| B. | 命题“若x2-3x+2=0,则x=1”的逆否命题为:“若x≠1,则x2-3x+2≠0” | |
| C. | 若复合命题p∨q为假命题,则p,q都是假命题 | |
| D. | “y<2”是“向量$\overrightarrow{a}$=(1,2),$\overrightarrow{b}$=(-2,y-4)之间的夹角为钝角”的充要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 分组 | [29.86,29.90) | [29.90,29.94) | [29.94,29.98) | [29.98,30.02) | [30.02,30.06) | [30.06,30.10) | [30.10,30.14) |
| 频数 | 29 | 71 | 85 | 159 | 76 | 62 | 18 |
| 分组 | [29.86,29.90) | [29.90,29.94) | [29.94,29.98) | [29.98,30.02) | [30.02,30.06) | [30.06,30.10) | [30.10,30.14) |
| 频数 | 12 | 63 | 86 | 182 | 92 | 61 | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | $\frac{16}{27}$ | D. | $\frac{32}{27}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{3\sqrt{2}}}{4}$ | B. | -$\frac{{\sqrt{2}}}{4}$ | C. | -$\frac{{3\sqrt{2}}}{4}$ | D. | $\frac{{\sqrt{2}}}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com