Question

已知函数y=f（x），任取t∈R，定义集合：At={y|y=f(x)，点P(t，f(t))，Q(x，f(x))，|PQ|≤

2

}．设M_t，m_t分别表示集合A_t中元素的最大值和最小值，记h（t）=M_t-m_t．则：
（1）若函数f（x）=x，则h（1）=

 

；
（2）若函数f(x)=sin

π

2

x，则h（t）的最大值为

 

．

Answer 1

分析：（1）若函数f（x）=x，则点P（t，t），Q（x，x），根据|PQ|≤

2

，求得 1-t≤x≤t+1，即M_t =1+t，m_t =1-t，由此可得h（1）的值．
（2）画出函数f（x）=sin

π

2

，画出函数的图象，分析点P在曲线上从A接近B，从B接近C，从C接近D时，从D接近E时，h（t）值的变化情况，从而得到 h（t）的最小正周期，可得h（t）的最大值．

解答：解：（1）若函数f（x）=x，则 点P（t，t），Q（x，x），
∵|PQ|≤

2

，∴

(x-t)2+(x-t)2

≤

2

，
化简可得|x-t|≤1，-1≤x-t≤1，即 1-t≤x≤t+1，
即M_t =1+t，m_t =1-t，
∵h（t）=M_t-m_t ，
∴h（1）=（1+1）-（1-1）=2．
（2）若函数f（x）=sin

π

2

x，此时，函数的最小正周期为

2π

π 2

=4，点P（t，sin

π

2

t），Q（x，sin

π

2

x），
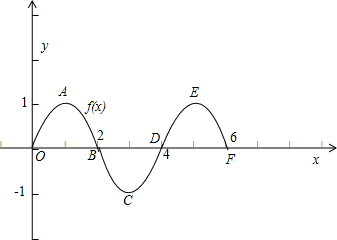
如图所示：
当点P在A点时，点O在曲线OAB上，M_t=1，m_t=0，h（t）=M_t-m_t=1．
当点P在曲线上从A接近B时，h（t）逐渐增大，当点P在B点时，M_t=1，m_t=-1，h（t）=M_t-m_t=2．
当点P在曲线上从B接近C时，h（t）逐渐见减小，当点P在C点时，M_t=1，m_t=0，h（t）=M_t-m_t=1．
当点P在曲线上从C接近D时，h（t）逐渐增大，当点P在D点时，M_t=1，m_t=-1，h（t）=M_t-m_t=2．
当点P在曲线上从D接近E时，h（t）逐渐见减小，当点P在E点时，M_t=1，m_t=0，h（t）=M_t-m_t=1．
…依此类推，发现 h（t）的最小正周期为2，最大值为2．
故答案为：2，2．

点评：本题主要考查函数的周期性，考查新定义，体现了数形结合以及分类讨论的数学思想，属于中档题．