
【题目】2018年2月22日.在平昌冬奥会短道速滑男子500米比赛中.中国选手武大靖以连续打破世界纪录的优异表现,为中国代表队夺得了本届冬奥会的首枚金牌,也创造中国男子冰上竞速项目在冬奥会金牌零的突破.某高校为调查该校学生在冬奥会期间累计观看冬奥会的时间情况.收集了200位男生、100位女生累计观看冬奥会时间的样本数据(单位:小时).又在100位女生中随机抽取20个人.已知这20位女生的数据茎叶图如图所示.
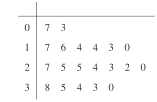
(1)将这20位女生的时间数据分成8组,分组区间分别为![]() ,在答题卡上完成频率分布直方图;
,在答题卡上完成频率分布直方图;
(2)以(1)中的频率作为概率,求1名女生观看冬奥会时间不少于30小时的概率;
(3)以(1)中的频率估计100位女生中累计观看时间小于20个小时的人数.已知200位男生中累计观看时间小于20小时的男生有50人请完成答题卡中的列联表,并判断是否有99 %的把握认为“该校学生观看冬奥会累计时间与性别有关”.
| 0.10 | 0.05 | 0.010 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |
附:![]() .
.
【答案】(1)见解析(2)![]() (3)有99%的把握
(3)有99%的把握
【解析】分析:(1)由题意知样本容量为![]() ,得到频率分布表,进而得到频率分布直方图.
,得到频率分布表,进而得到频率分布直方图.
(2)因为(1)中![]() 的频率为
的频率为![]() ,进而得到
,进而得到![]() 名女生观看冬奥会时间不少于
名女生观看冬奥会时间不少于![]() 小时的概率;
小时的概率;
(3)因为(1),根据题意,得出![]() 列联表,求得
列联表,求得![]() 的值,即可作出判断.
的值,即可作出判断.
详解:解:(1)由题意知样本容量为![]() ,频率分布表如下:
,频率分布表如下:
分组 | 频数 | 频率 |
|
| 1 |
| 0.01 |
| 1 |
| 0.01 |
| 4 |
| 0.04 |
| 2 |
| 0.02 |
| 4 |
| 0.04 |
| 3 |
| 0.03 |
| 3 |
| 0.03 |
| 2 |
| 0.02 |
合计 | 20 | 1 |
频率分布直方图为:
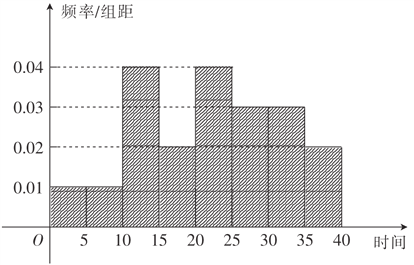
(2)因为(1)中![]() 的频率为
的频率为![]() ,
,
所以![]() 名女生观看冬奥会时间不少于
名女生观看冬奥会时间不少于![]() 小时的概率为
小时的概率为![]() .
.
(3)因为(1)中![]() 的频率为
的频率为![]() ,故可估计
,故可估计![]() 位女生中累计观看时间小于
位女生中累计观看时间小于![]() 小时的人数是
小时的人数是![]() .所以累计观看时间与性别列联表如下:
.所以累计观看时间与性别列联表如下:
男生 | 女生 | 总计 | |
累计观看时间小于20小时 | 50 | 40 | 90 |
累计观看时间不小于20小时 | 150 | 60 | 210 |
总计 | 200 | 100 | 300 |
结合列联表可算得
![]() ,
,
所以,有![]() 的把握认为“该校学生观看冬奥会累计时间与性别有关”.
的把握认为“该校学生观看冬奥会累计时间与性别有关”.


科目:高中数学 来源: 题型:
【题目】某单位从一所学校招收某类特殊人才,对![]() 位已经选拔入围的学生进行运动协调能力和逻辑思维能力的测试,其测试结果如下表:
位已经选拔入围的学生进行运动协调能力和逻辑思维能力的测试,其测试结果如下表:

例如,表中运动协调能力良好且逻辑思维能力一般的学生有![]() 人.由于部分数据丢失,只知道从这
人.由于部分数据丢失,只知道从这![]() 位参加测试的学生中随机抽取一位,抽到运动协调能力或逻辑思维能力优秀的学生的概率为
位参加测试的学生中随机抽取一位,抽到运动协调能力或逻辑思维能力优秀的学生的概率为![]() .
.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)从参加测试的![]() 位学生中任意抽取
位学生中任意抽取![]() 位,求其中至少有一位运动协调能力或逻辑思维能力优秀的学生的概率;
位,求其中至少有一位运动协调能力或逻辑思维能力优秀的学生的概率;
(III)从参加测试的![]() 位学生中任意抽取
位学生中任意抽取![]() 位,设运动协调能力或逻辑思维能力优秀的学生人数为
位,设运动协调能力或逻辑思维能力优秀的学生人数为![]() ,求随机变量
,求随机变量![]() 的分布列.
的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,AB//CD,且![]() .
.

(1)证明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC, ![]() ,求二面角A-PB-C的余弦值.
,求二面角A-PB-C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的定义域是
的定义域是![]() ,对任意
,对任意![]() ,当
,当![]() 时,
时,![]() .关于函数
.关于函数![]() 给出下列四个命题:①函数
给出下列四个命题:①函数![]() 是周期函数;②函数
是周期函数;②函数![]() 是奇函数;③函数
是奇函数;③函数![]() 的全部零点为
的全部零点为![]() ;④当
;④当![]() 时,函数
时,函数![]() 的图象与函数
的图象与函数![]() 的图象有且只有三个公共点.其中真命题的序号为__________.
的图象有且只有三个公共点.其中真命题的序号为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面几何中,研究三角形内任意一点与三边的关系时,有真命题:边长为![]() 的正三角形内任意一点到各边的距离之和是定值
的正三角形内任意一点到各边的距离之和是定值![]() 。类比上述命题,请写出关于正四面体内任意一点与四个面的关系的一个真命题,并给出证明。
。类比上述命题,请写出关于正四面体内任意一点与四个面的关系的一个真命题,并给出证明。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com