练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    设f(x)是(-∞,+∞)上的奇函数,且f(x+2)=-f(x),下面关于f(x)的判定:其中正确命题的序号为　　　　.

    ①f(4)=0;

    ②f(x)是以4为周期的函数;

    ③f(x)的图象关于x=1对称;

    ④f(x)的图象关于x=2对称.

     

    ①②③

    【解析】∵f(x+2)=-f(x),

    ∴f(x)=-f(x+2)=-(-f(x+2+2))=f(x+4),

    即f(x)的周期为4,②正确.

    ∴f(4)=f(0)=0(∵f(x)为奇函数),即①正确.

    又∵f(x+2)=-f(x)=f(-x),

    ∴f(x)的图象关于x=1对称,∴③正确.

    又∵f(1)=-f(3),当f(1)≠0时,显然f(x)的图象不关于x=2对称,∴④错误.

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2014年高考数学文二轮专题复习与测试选修4-5不等式选讲练习卷（解析版） 题型：解答题

    设不等式|x－2|<a(a∈N*)的解集为A，且∈A，∉A.

    (1)求a的值；

    (2)求函数f(x)＝|x＋a|＋|x－2|的最小值．

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学文二轮专题复习与测试解答题抢分训练练习卷（解析版） 题型：解答题

    设L为曲线C：y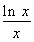＝在点(1,0)处的切线．

    (1)求L的方程；

    (2)证明：除切点(1,0)之外，曲线C在直线L的下方．

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学全程总复习课时提升作业（四）第二章第一节练习卷（解析版） 题型：填空题

    已知两个函数f(x)和g(x)的定义域和值域都是集合{1,2,3},其函数对应关系如下表:

    则方程g(f(x))=x的解集为____________.

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学全程总复习课时提升作业（四）第二章第一节练习卷（解析版） 题型：选择题

    设f(x)=则f(5)的值为(　　)

    (A)10　　　(B)11　　　(C)12　　　(D)13

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学全程总复习课时提升作业（六）第二章第三节练习卷（解析版） 题型：选择题

    设f(x)是连续的偶函数,且当x>0时是单调函数,则满足f(x)=f()的所有x之和为(　　)

    (A)-3　　　(B)3　　　(C)-8　　　(D)8

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学全程总复习课时提升作业（六）第二章第三节练习卷（解析版） 题型：选择题

    设函数f(x)和g(x)分别是R上的偶函数和奇函数,则下列结论恒成立的是(　　)

    (A)f(x)+|g(x)|是偶函数

    (B)f(x)-|g(x)|是奇函数

    (C)|f(x)|+g(x)是偶函数

    (D)|f(x)|-g(x)是奇函数

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学全程总复习课时提升作业（八）第二章第五节练习卷（解析版） 题型：选择题

    函数f(x)=1+log2x,f(x)与g(x)=21-x在同一直角坐标系下的图象大致是(　　)

     

     

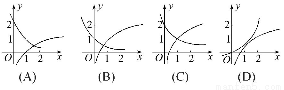
    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学全程总复习课时提升作业（九）第二章第六节练习卷（解析版） 题型：选择题

    已知函数f(x)=x2+1的定义域为[a,b](a<b),值域为[1,5],则在平面直角坐标系内,点(a,b)的运动轨迹与两坐标轴围成的图形的面积为(　　)

    (A)8 (B)6 (C)4 (D)2

     

    查看答案和解析>>

    同步练习册答案